Enunciado
Cálculo Numérico - Franco e Neide B - Cálculo Numérico- Ed: 1º - Capítulo 11.Exercícios - Ex. 12
Determine h de modo que a regra do trapézio forneça o valor de:
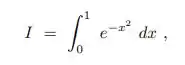
Com erro inferior a .
Passo 1
Opa! Tudo beleza? Neste exercício, já iremos começar a trabalhar um pouquinho com erros nos métodos de integração. Especificamente nesta questão, iremos usar a formulinha para o erro da regra do trapézio, que vai nos auxiliar a encontrar o melhor passo (h) para alcançar a precisão desejada no valor da integral. Podemos achar o erro da seguinte forma:
O erro total é menor ou igual que o passo ao cubo dividido por doze, multiplicado pela derivada segunda da função presente na integral aplicada ao ponto que maximiza seu valor.Com isso, podemos partir para os cálculos.
Passo 2
Agora vamos calcular as derivadas de :
Aplicando no intervalo de integração , vamos descobrir que o valor máximo da derivada segunda é quando x = 1, onde obtemos aproximadamente 0.73575 . Bora finalizar calculando o h, já que temos tudo o que precisamos:
Desta relação tiramos que:
Com um passo pequeno como este, pode ter certeza de que o valor da integral vai ser muito preciso, assim como o exercício pediu. Até o próximo!
Resposta
.