Método de Jacobi-Richardson
Produzido por Bruno PestanaTeoria
Introdução aos métodos iterativos
Fala meus jovenzitos, tudo na boa? Vamos começar agora, um assunto que é show de bola, mas que as vezes não é muito valorizado. Algumas universidades nem estudam o coitado, se você não vê esse conteúdo na facul ou não é um mega curioso e louco por aprendizado... pode pular para o próximo conteúdo que é bem convencional.

Agora, se você é do grupo que precisa aprender ou tá curioso com esse negócio, vem comigo que é só sucesso!!!! A primeira coisa que vamos fazer, é retomar conceitos sobre métodos iterativos que abordamos em outros conteúdos, e se você não lembra tá tudo bem!
Vamos partir do mais abstrato possível. Os métodos iterativos funcionam através das iterações, que são basicamente etapas para encontrar uma resposta. E essas etapas sempre dependem das etapas anteriores. Até aí tudo ok né?
Uma coisa importante nos métodos iterativos é que precisamos sempre saber se o resultados que estamos conseguindo a cada iteação está convergindo para a solução real ou não. E para saber se estamos “chegando lá” temos critérios de parada que vai nos guiar e falar “hey filhão, já pode parar aí beleza?” ou até mesmo “Amada, pare agora”.
Agora que conseguimos dar uma pincelada em conceitos bem importantes, vamos para o que interessa aqui. Que raios é o método de Jacobi-Richardson? Esse maluco é o mesmo do Gauss-Jacobi? Hahhahahaaha

Vem comigo, que vamos aprender a calcular essa parada aí!
Jacobi-Richardson
O método de Jacobi-Richardson é um método iterativo para resolver sistemas lineares. Tá, mas como é que ele vai fazer isso?
Imagine que nós temos um sistema qualquer de .
Por exemplo:
Mas a nossa matriz pode ter ordem de linhas e colunas!
De acordo com o Jacobi-Richarson a nossa matriz A do sistema, pode ser separada em:
Onde :
: Matriz triangular inferior formada pela parte inferior de A;
: Matriz diagonal formada pela diagonal de A;
: Matriz triangular superior formada pela parte superior de A.
Representando em termos de matriz, fica mais ou menos assim:
A nossa matriz :
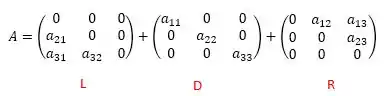
Através de uma séeeeerie de cálculos e modificações matemáticas, e entendendo que o , conseguimos chegar na nossa queridinha função iteração:
Maaaas, por via de regra e para facilitar nossa vida, são feitas mais algumas modificações para que a gente não tenha que calcular D:
E é com essa função que ós iremos trabalhar!
Aqui nesse processo iterativo de Jacobi-Richardson, vamos convergir de modo que:
Mas não se desespere, você já vai ver que tudo nesse mundo ainda faz sentido. Afinal, antes de calcularmos o sistema, temos que cumprir um passo muito importante: ver se o nosso sistema satisfaz o critério de convergência!
Alô Alô Convergência!
Acabamos de embarcar num ponto importantíssimo do nosso problema, ver se o sistema satisfaz ou não o critério de convergência, que é basicamente o que vai garantir se nós podemos achar a solução do probleminha ou não!
O primeiro critério a ser atendido é: a nossa matriz é diagonal dominante ?
Eita! Como assim?
Um matriz diagonal dominante tem o módulo do elemento da diagonal maior que a soma dos módulos de todos os outros elementos da linha, se esse critério é atendido, nós automaticamente matamos todos os outros e
Então, o critério das linhas será satisfeito se:
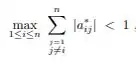
Isso tudo, até a ordem n.
Uma coisa importante aqui é, devemos atender pelo menos um dos critérios para poder efetuar os cálculos.
O próximo critério é o critério das linhas : Para calcular o critério das linhas, devemos primeiro retornar a nossa matriz e vamos pegar o termo dominante de cada linha (linha 1: , linha 2:, linha 3: ). E dividiremos os demais temos pelos termos dominantes, por exemplo:
MARCA BEM ESSE PASSO, USAREMOS EXATAMENTE O MESMO NO CRITÉRIO DAS COLUNAS!
Alíás, se a matriz tiver a extensão b, nós calculamos um b novo para cada linha também beleza? É só dividir o valor de b atual, pelo valor do termo “dominante”.
Aí então, montamos um novo sisteminha com essa alteração e também fazemos a norma dos termos da mesma linha (exceto o termo dominante):
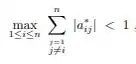
O máximo valor obtido da soma de cada um desses grupos deve ser menor que 1!
E por fim, temos o critério das coluna! O critério das colunas vai usar aqueles temos que calculamos no critério das linhas, a única diferença é que dessa vez somaremos os termos que pertencem a cada coluna (com exceção do termo dominante), assim:
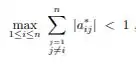
O critério continua valendo, o máximo valor obtido da soma de cada um desses grupos deve ser menor que 1!
Bora Calcular!
Agora nós já aprendemos a definir os critérios de convergência, para calcular, nós montamos uma matriz nova né? Com essa carinha aqui:
Sabe qual é a nossa função iteração?
EXATAMENTE, o nosso sistema!
Quer dizer que é só montar o sisteminha maroto e resolver????
ISSO MEXXXXXXMO!
Geralmente, o prof vai te dar um conjunto de valores iniciais, você vai basicamente jogar esses valores no lugar de até chegar em um valor novo de , aí você vê se atendeu o critério de parada ou não. Aí meu caro, se não atender ao critério, você usa esses valores novos de até atingir o critério de parada.

É só olhar na tabelinha, e ver qual quem será meu novo valor a ser usado.
E qual é o critério de parada?
Os erros absolutos e relativos, entre cada termo:
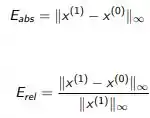
Vamos fazer exercício, que vai ficar bem mais fácil de entender!
Alô Alô Convergência!
Bora Calcular!
Exercícios Resolvidos
Exercício Resolvido #1
Adaptado livro de Cálculo Numérico UFF- Jacumina
Utilize os critérios das linhas para garantir convergência:
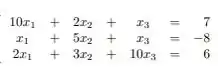
Passo 1
Um ponto importante em Jacobi-Richardson é que o critério das linhas será satisfeito se:
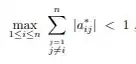
Na verdade, diferente de outros métodos, se nós conseguirmos garantir qualquer um, tipo, qualquer critério mesmo...Pasme, aí garantimos a convergência.

É isso mesmo, garantir um critério só já é sucesso.
Vemos que uma matriz qualquer A é estritamente diagonar dominante se a soma dos termos da linha for menor (em módulo) que o termo dominante da linha
Tendo o nosso sistema:
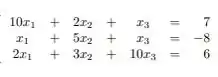
Existem duas maneiras de satisfazer o critério das linhas, primeiro é testar se a matriz é estritamente diagonal dominante e o outro falaremos no passo 2.
Vamos entender em termos de linhas e colunas:
Agora, testaremos se a matriz é estritamente dominante:
Apenas com esse critério, já garantimos que Jacobi-Richardson pode ser implementado!
Passo 2
Para calcular o critério das linhas propriamente dito, voltaremos láaaaaa pra nossa matriz:
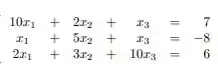
Faremos o seguinte, vamos pegar o termo dominante de cada linha (linha 1: , linha 2:, linha 3: ). E dividiremos os demais temos pelos termos dominantes:
Montando a função temos:
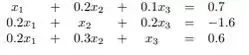
Mesmo não sendo necessário, já que garantimos a convergência no passo anterior, podemos calcular novamente os módulos assim:
Perceba que 0,5 foi o maior valor obtido, então é o nosso máximo, e o valor máximo deve ser sempre menor que 1. Então se 0,5
Resposta
Critério atendido
Exercício Resolvido #2
Adaptado livro de Cálculo Numérico UFF- Jacumina
Ainda com o exercício anterior, calcule o critério de colunas necessário para garantir a convergência:
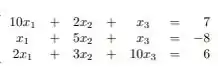
Passo 1
Apesar de sabermos que o critério das linhas e da dominância já foram atendidos, é importante aprender a calcular o critério das colunas também.
Tendo o nosso sistema:
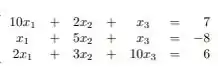
Masssss, vamos usar a função divisão que obtivemos no exercício anterior:
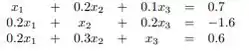
Mas como o nome do método já diz, testaremos as colunas
Nesse caso, 0,5
Apenas com esse critério, já garantimos que Jacobi-Richardson pode ser implementado!
Resposta
Critério atendido
Exercício Resolvido #3
Adaptado livro de Cálculo Numérico UFF- Jacumina
Utilize os critérios das linhas para garantir convergência:
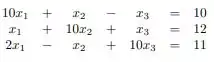
Passo 1
Um ponto importante em Jacobi-Richardson é que o critério das linhas será satisfeito se:
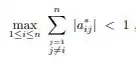
Para calcular o critério das linhas propriamente dito, voltaremos láaaaaa pra nossa matriz:
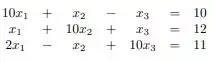
Faremos o seguinte, vamos pegar o termo dominante de cada linha (linha 1: , linha 2:, linha 3: ). E dividiremos os demais temos pelos termos dominantes:
Passo 2
Mesmo não sendo necessário, já que garantimos a convergência no passo anterior, podemos calcular novamente os módulos assim:
Perceba que 0,3 foi o maior valor obtido, então é o nosso máximo, e o valor máximo deve ser sempre menor que 1. Então se 0,3
Resposta
Critério atendido
Exercício Resolvido #4
Adaptado de Cálculo Numérico, Resolução de Sistemas Lineares da UFMG
Agora, utilize os critérios das colunas para garantir convergência:
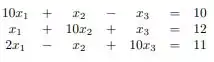
Passo 1
Apesar de sabermos que o critério das linhas e da dominância já foram atendidos, é importante aprender a calcular o critério das colunas também.
Tendo o nosso sistema:
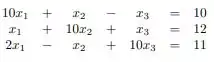
Masssss, vamos usar a função divisão que obtivemos no exercício anterior:
Mas como o nome do método já diz, testaremos as colunas
Nesse caso, 0,2
Apenas com esse critério, já garantimos que Jacobi-Richardson pode ser implementado!
Resposta
Critério atendido
Exercício Resolvido #5
Adaptado de Cálculo Numérico, Resolução de Sistemas Lineares da UFMG
Utilize os critérios das linhas para garantir convergência:
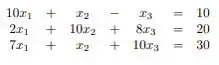
Passo 1
Um ponto importante em Jacobi-Richardson é que o critério das linhas será satisfeito se:
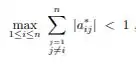
Para calcular o critério das linhas propriamente dito, voltaremos láaaaaa pra nossa matriz:
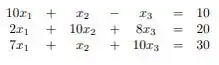
Faremos o seguinte, vamos pegar o termo dominante de cada linha (linha 1: , linha 2:, linha 3: ). E dividiremos os demais temos pelos termos dominantes:
Passo 2
Podemos calcular novamente os módulos assim:
Perceba que 1 foi o maior valor obtido, então é o nosso máximo, e o valor máximo deve ser sempre menor que 1. Então se 1 = 1 o nosso critério não foi antendido.
Resposta
Critério não atendido