Otimização – Casos Clássicos
Teoria
Olá, galerinha! Relembrando, otimização é o processo de encontrar a melhor solução para um problema, e fazemos isso achando valores máximos ou mínimos. Então, existem alguns casos clássicos que podem aparecer na sua prova e você já conhecendo ele, vai ajudar muito. E é isso que vamos ver agora!
Pitágoras
Imagine um rio com 10 metros de margem, onde um velho nadador chamado Phelps quer ir de um ponto A de um lado do rio para um ponto B do outro lado do rio que está há uma distância horizontal de do ponto A, como indicado na figura.
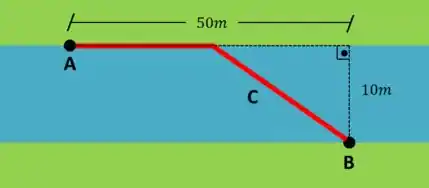
Ele pode caminhar até certo ponto e depois atravessar o rio nadando na diagonal, fazendo o trajeto indicado em vermelho. Se Phelps anda a e nada a , qual o melhor trajeto de Phelps?
Repara que nossa figura formou um triângulo de Pitágoras. E esse é o nosso primeiro caso clássico, então vamos resolver!
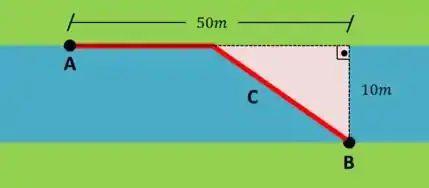
Na maioria das questões de otimização, a função a otimizar e outras equações não são fornecidas no enunciado. Então, nós vamos ter que analisar o problema e encontrar a função a otimizar e outras equações. Vamos lá?
1º Passo: Fazer um desenho do problema e atribuir variáveis para as quantidades pedidas. Mas isso o problema já nos forneceu, né? Então vamos seguindo
2º Passo: Escrever relações entre as variáveis do problema.
Vamos primeiro destacar o triângulo retângulo que é o foco do nosso problema e adotar uma variável , para tentaremos achar a relação entre e .
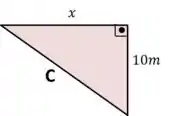
Usando Pitágoras:
Ou seja, é a distância que Phelps nada. Consequentemente, a distância que ele andará será o comprimento da margem (50 metros) menos a distância . Então a distância que ele anda em terra é
3º Passo: Escrever a função a ser otimizada!
Repara que o tempo que ele leva no trajeto é o somatório da variação de tempo em terra (andando) com a variação de tempo no rio (nadando). Então a função a ser otimizada será,
Lá dá física do ensino médio e já substituindo:
Da mesma maneira:
Aí pronto:
A partir daqui, é só fazer como na teoria inicial de otimização!
4º Passo: Achar os pontos de máximo (se quero maximizar) ou de mínimo (se quero minimizar).
Para isso, nós temos que derivar essa função, pois tanto pra pontos de máximo quanto pra pontos de mínimo, a reta tangente à eles será horizontal, ou sejaaaa, o coeficiente angular delas é zero.
Primeiro, vamos reescrever a nossa equação para facilitar na hora de derivar,
Derivando,
Agora vamos igualar a zero,
Vamos deixar essa equação com uma cara mais simples, segue os passos
Resolvendo a equação de segundo grau chegamos que,
5º Passo: Verificar se o ponto achado é um ponto de máximo (ou mínimo) local ou global. No fundo, se existe algum ponto melhor (que é “mais máximo” ou “mais mínimo” do que o ponto achado anteriormente). Para isso, teste os extremos do intervalo ou estude o comportamento.
Como a nossa função trata-se de uma equação de segundo grau, só um mínimo (ou máximo) global! É só lembrar da cara de uma equação de segunda grau que é uma parábola para cima ou para baixo.
Então, galerinha, já resolvemos o problema!
Distância de Ponto à Função
Agora vamos dificultar um pouco! No problema acima, a gente desenhou o que tava acontecendo, chegamos a um triangulo retângulo e aplicamos Pitágoras. Mas em alguns casos, nós iremos conseguir ver isso tão fácil e é isso que vamos ver agora.
Olha essas duas funções aqui, e :
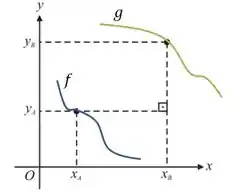
Se eu te pedisse a menor distância entre as duas funções, chamando um ponto de qualquer de e um ponto qualquer de de , como você começaria?
Vou começar dando uma melhorada no desenho:
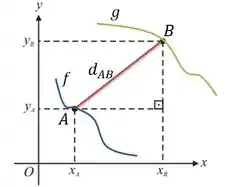
Se os pontos e são pontos das curvas e , então a distância entre os pontos formará um triângulo retângulo e poderá ser calculada por Pitágoras. A gente pode seguir o passo a passo descrito acima.
Para achar a equação a ser otimizada, vamos chamar a distância de . Então por Pitágoras:
Isolando e substituindo por seu valor como função de :
Simples assim, basta usar essa fórmula para otimizar a distância entre duas curvas! Neste caso, como queremos a menor distância, vamos atrás do mínimo.
Quando precisar encontrar a menor distância entre um ponto e uma curva a distância entre eles também será dada pela diferença entre as coordenadas aplicadas ao Pitágoras.
Vamos de um exemplo! A gente quer encontrar o ponto na reta que está mais próximo da origem .
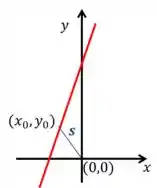
Nós já conhecemos um ponto e queremos achar outro . Então um será o nosso e o outro o nosso . E repara que o nosso é a nossa . Vamos jogar na nossa equação,
Agora, vamos derivar para achar o nosso mínimo e igualar a zero para achar o nosso mínimo.
Agora que achamos , vamos achar o nosso jogando na equação da reta que nos foi dada:
Então o ponto na reta que está mais próximo da origem é o .
Área e Volume
Um homem do campo tem 1.500 de cerca e quer construir um cercado retangular em volta do seu terreno. Qual é a área máxima que ele poderá cercar? Qual será a altura e a largura da área cercada? Como equaciona esse treco, amigo?
Bem, identificamos que se trata de um problema de otimização, pois queremos a área máxima.
1º Passo: Faça um desenho do problema e atribua variáveis para as quantidades pedidas.
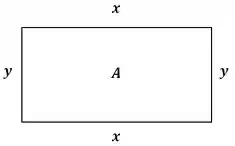
2º Passo: Escreva relações entre as variáveis do problema.
3º Passo: Escrever a função a ser maximizada (ou minimizada) em função de apenas uma das variáveis do problema. Como fica a área em função de ?
4º Passo: Derive a função e iguale a para achar os pontos de máximo (ou de mínimo).
5º Passo: Verificar se o ponto achado é um ponto de máximo (ou mínimo) local ou global.
Opa! Novamente, a nossa função trata-se de uma equação de segundo grau, ou seja, s um máximo global! Então as dimensões são e e a área máxima é
Tudo bem? Outros problemas de área e perímetro cobram outras fórmulas, então fique ligado!
Grave todas essas fórmulas aí!
Volume
E se fosse um volume? Problemas de volume em nada mudam quanto à organização do passo-a-passo, mas você precisa saber as principias fórmulas cobradas:
Veremos bastante disso nos exercícios de fixação ;-).
Distância de Ponto à Função
Área e Volume
Volume
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ - Cálculo 1 - P2 2012.1 - 1
Seja uma reta passando pelo ponto com inclinação negativa. Dentre todos os triângulos retângulos obtidos tomando e a interseção da reta com o primeiro quadrante, encontre as dimensões do que possui a menor hipotenusa.
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
Esta questão merece um desenho bem feito:
Agora sim podemos começar à pensar. Atribuindo algumas dimensões ao problema
Passo 2
Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
Repare que existem dois triângulos semelhantes na figura do problema:
O triângulo em vermelho tem altura e base . O triângulo em azul tem altura e base . Como são semelhantes, podemos usar a semelhança de triângulos:
Passo 3
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Queremos achar a menor hipotenusa que será dada por Pitágoras:
Passo 4
Derivamos essa função e achamos os pontos críticos.
Igualando à zero obtemos:
Sumindo com esse denominador que nunca vai poder ser zero ficamos com:
Também teremos outro ponto crítico em que é onde a derivada não existe. Nesse ponto, porém, a reta seria vertical e não tocaria o eixo . Vamos desconsiderá-lo então.
Passo 5
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Agora precisamos provar que é um mínimo. Uma alternativa é o teste da derivada segunda, a outra é simplesmente analisar o sinal da derivada . O segundo teste é mais conveniente, pois derivar isso aí de novo seria bem complicado.
Arrumando, podemos ver que o denominador não influencia no sinal. Por ser uma raiz ele deve ser sempre positivo.
Vamos testar um ponto à esquerda e à direita do ponto crítico. Pode ser e . Como o sinal só depende do numerador basta testar somente ele.
Para
Para :
A derivada é negativa à esquerda e positiva à direita, então temos um ponto de mínimo aí!
Passo 6
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Temos um outro ponto crítico em , mas nesse ponto, a reta é vertical e não toca o eixo . A hipotenusa, portanto, será infinita. Maior que nosso ponto de mínimo, obviamente.
Passo 7
Pegamos o melhor ponto crítico obtido no passo e comparamos com os valores na fronteira da função. O melhor valor de todos será o valor ótimo.
vai variar desde , que é seu valor mínimo, até infinito. Já vimos o que acontece em . Para :
Como ambas fronteiras vão para mais infinito, garantimos que o nosso ponto de mínimo encontrado é mínimo global!
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração Própria
Uma cerca de de altura corre paralela a um edifício alto a uma distância de do edifício. Qual o comprimento da menor escada que se apoie no chão e na parede do prédio por cima da cerca?
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
Ok, primeira coisa que temos que notar é que a análise desse problema começa por um corte perpendicular à extensão da cerca. Imagina como se eu tivesse olhando para cerca e para o edifício no sentido em que eles correm, como isso aqui, ó:
Beleza, a partir daqui já aparece um triângulo e umas distâncias relevantes para o nosso problema. Só para esclarecer tudo, a distância mínima dessa escada tem que, necessariamente, estar tocando ali no pico do arame, já que é o ponto no qual ele mais se “aproxima” do chão e da parede.
Passo 2
Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
O cara quer o tamanho mínimo da escada, ou seja, precisamos descrever a escada de através de alguma equação. Bom, imagina que eu chamo a distância do ponto onde ela toca o edifício de e a distância do ponto onde ela toca o chão de . Bom, por Pitágoras, eu poderia dizer que o comprimento da escada é:
Tá maneiro, e como eu chego aos valores de e de ? Nesse desenho aqui eu chamei de a distância do ponto onde a escada toca o chão até a cerca. Marquei também as distâncias que o problema me deu:
Repara, por aqui, eu tenho:
E posso matar essa altura por semelhança de triângulos, certo?
Passo 3
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Jogando na equação do :
Passo 4
Derivamos essa função e achamos os pontos críticos.
Vamos derivar agora, e o negócio fica assim:
Ok, como o denominador é uma raiz da soma de quadrados, será sempre positivo. Então podemos zerar só a parte de cima e ver no que vai dar:
Multiplicamos tudo por e dei uma ajeitada:
Assim, os valores de são:
Como não pode ser negativo, o ponto crítico é
Passo 5
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Para provar que esse é ponto de mínimo, olhamos para o sinal de antes e depois do ponto. Ora, lembrando que a parte do denominador é sempre positiva, vou fazer a análise de sinal de
Essa parte corresponde ao numerador, e posso afirmar que é maior que quando e é maior enquanto . Fazendo um quadro de sinais:
Olhando para os valores próximos a , a derivada é negativa antes e positiva depois, caracterizando um ponto de mínimo.
Passo 6
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Não temos outros pontos críticos a considerar aqui.
Passo 7
Pegamos o melhor ponto crítico obtido no passo e comparamos com os valores na fronteira da função. O melhor valor de todos será o valor ótimo.
Uma da função é a escada encostada na cerca . Nesse ponto, a escada não vai encostar no prédio, então desconsideramos.
A outra fronteira é com a escada apoiada no topo da cerca, onde . Nessas condições, o comprimento da escada também tenderá a infinito.
Dessa maneira, o ponto crítico que encontramos é o ponto de mínimo global.
Para finalizar, temos que descobrir a , sendo esse o menor comprimento da escada:
Eu sei, resultado feio que dói, dá até nojo chegar num negócio assim. Mas Cálculo não é coisa de moleque, tem que ter peito e responsa para chegar nisso aqui e confiar.
Resposta
Exercício Resolvido #3
George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp. 216-55. MODIFICADO
Sejam e as funções deriváveis traçadas aqui. O ponto é onde a distância vertical entre as curvas é máxima. Há algo de especial em relação às tangentes às duas curvas em ? Justifique sua resposta.
Passo 1
Temos que o ponto será um ponto de mínimo da distância entre os dois. Essa distância é puramente vertical, então:
Sendo a distância.
Passo 2
estará presente em um dos pontos críticos. Então vamos derivar:
Passo 3
Pontos críticos ocorrem onde a derivada não existe ou é zero. Ela sempre vai existir, pois e são deriváveis. Então, resta zero:
Passo 4
será o ponto onde as derivadas são iguais. Agora vamos relembrar a equação da reta tangente a cada curva?
Se as derivadas são iguais, as retas tangentes a e diferem apenas da quantidade e . Portanto, elas tem a mesma inclinação, mas diferem na translação, ou seja, são retas paralelas.
Resposta
Retas tangentes paralelas
Exercício Resolvido #4
James Stewart, Cálculo Vol. 1, 6ª ed. São Paulo: Cengage Learning, 2010, pp 308 - 17
Encontre o ponto sobre a reta que está mais próximo da origem.
Passo 1
Vamos por partes.
O problema pede que achemos o ponto que pertença à reta e que seja o mais próximo possível da origem . Ou seja, temos que minimizar a função distância do ponto até a origem.
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
A reta está em vermelho no desenho acima. O segmento de reta preto ilustra a distância de um ponto qualquer da reta e a origem.
Passo 2
Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
Vale lembrarmos a fórmula da distância entre dois pontos.
Seja o ponto 1 e o ponto 2 . A distância entre eles é dada por:
No nosso caso aqui, temos o ponto e a origem . Aplicando a fórmula da distância:
Outra relação importante é o fato de o ponto pertencer à reta . Portanto:
Passo 3
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Queremos minimizar a função distância :
E sabemos que:
Substituindo:
Passo 4
Derivamos essa função e achamos os pontos críticos.
Como a raiz do denominador é positiva por ser uma raiz quadrada, então basta fazermos:
O denominador é sempre positivo, pois não tem raízes reais.
Passo 5
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Vamos analisar a função:
Usando o teste da primeira derivada, podemos ver que para todo e para todo . Portanto, é realmente um ponto de mínimo.
Passo 6
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Não temos outros pontos críticos a destacar aqui.
Passo 7
As fronteiras para são as fronteiras para a reta, ou seja, e . É fácil notar que quando a reta vai para os extremos, a distância para a origem aumenta cada vez mais. A menor distância, portanto, é o valor encontrado no ponto crítico que será mínimo global.
Resposta
O ponto é .
Exercício Resolvido #5
James Stewart, Cálculo Vol. 1, 6ª ed. São Paulo: Cengage Learning, 2010, pp – 307 – 5
Encontre as dimensões de um retângulo com um perímetro de cuja área seja a maior possível.
Passo 1
É um problema de maximização. Temos que maximizar a função área. O problema nos deu o perímetro.
Vamos seguir o passo a passo para problemas de otimização.
1º Passo: Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
.
Passo 2
2º Passo: Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
O perímetro vai ser:
E a área:
Passo 3
3º Passo: Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Queremos maximizar a função área :
Passo 4
4º Passo: ivamos essa função e achamos os pontos críticos.
Passo 5
5º Passo: Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Vamos analisar a função:
Repare que a função é um polinômio de segundo grau e, portanto, é uma parábola voltada para baixo e só possui um ponto de máximo, que é o que achamos anteriormente. Logo:
Não precisamos de outros passos aqui, pois, por ser uma parábola voltada para baixo, esse é um ponto de máximo global.
Resposta
Trata-se de um quadrado de lado igual a .
Exercício Resolvido #6
UERJ - Cálculo 1 - Lista Derivadas – 6
Um campo retangular à margem de um rio deve ser cercado com exceção do lado ao longo do rio. Se o custo do material for de no lado paralelo ao rio e de nos dois extremos, ache o campo de maior área que possa ser cercado com de materiais.
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
Bom, comecei desenhando esse caso aí:
A área do retângulo, que é o formato do campo, vai ser dada por:
Passo 2
Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
Sendo que temos como limitante aquele preço de . Bom, se custa a cerca do lado paralelo e a dos outros dois, posso criar um custo, estando e em metros, dado por essa equação:
Repara que são dois lados de comprimento e um lado . Como ele diz que esse custo é fixo em , ficamos assim:
Passo 3
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Juntando a última equação à da área, tendo colocado o em evidência:
Passo 4
Derivamos essa função e achamos os pontos críticos.
Se eu procuro o ponto crítico da área, ou seja, a maior possível, devo derivar e igualar a esta equação:
Como é um polinômio, a derivada sempre vai existir.
Passo 5
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Como a derivada é fácil de calcular, é melhor derivar de novo e aplicar o teste da segunda derivada.
Como a segunda derivada é negativa, esse é um ponto de máximo.
Passo 6
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Não há outros pontos críticos a calcular, então, próximo passo!
Passo 7
Pegamos o melhor ponto crítico obtido no passo e comparamos com os valores na fronteira da função. O melhor valor de todos será o valor ótimo.
Olhando para função área:
Vemos que o menor valor para é zero, uma vez que é uma medida. O maior é . Para zero. A área é zero e inútil. Para :
O que também não é aplicável. Dessa maneira é um ponto de máximo global, onde:
Eu sei que é repugnante, mas esse é nosso resultado.
Resposta
Exercício Resolvido #7
James Stewart, Cálculo Vol. 1, 6ª ed. São Paulo: Cengage Learning, 2010, pp – 308-27
Encontre as dimensões do retângulo com a maior área que pode ser inscrito em um triângulo equilátero com lado se um dos lados do retângulo estiver sobre a base do triângulo.
Passo 1
Claramente é um problema de otimização. Temos que maximizar a área de um retângulo que pode ser inscrito em um triângulo equilátero, ou seja, que possui três lados iguais.
1º Passo: Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
Temos que os lados do triângulo equilátero valem e que os lados do retângulo inscrito valem e .
Passo 2
2º Passo: Temos que escrever equações que relacionam as variáveis do problema. Nesse passo, podem ser necessários conhecimentos básicos de geometria, trigonometria, etc.
Como relacionar , e ? Vamos desenvolver um pouco mais a figura para encontrarmos uma relação através do Teorema de Pitágoras. Repare:
O triângulo formado acima do retângulo também será um triângulo equilátero, já que seus ângulos são de . Portanto, repare que o triângulo formado pelas três bolinhas azuis na figura é um triângulo retângulo e, por isso, podemos aplicar Pitágoras:
Essa é a relação entre e . Lembrando que é um dado do problema. Ou seja, é como se o enunciado tivesse dado quanto vale o lado do triângulo equilátero. ou um número dá no mesmo. O nosso resultado ficará em função de . A área do retângulo é:
Passo 3
3º Passo: Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Queremos maximizar a função área :
E sabemos que:
Substituindo:
Passo 4
4º Passo: Derivamos essa função e achamos os pontos críticos.
Como é um polinômio, a derivada sempre existirá
Passo 5
5º Passo: Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Vamos analisar a função:
Usando o teste da primeira derivada, podemos ver que para todo e para todo . Portanto, é realmente um ponto de máximo global.
Nem precisamos dos outros passos, já mostramos que é global.
Resposta
As dimensões são e .
Exercício Resolvido #8
George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education do Brasil, 2009, pp. 311-14. MODIFICADO
Quais são as dimensões da mais leve lata em forma de cilindro reto, sem tampa, para conter exatamente .
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
Bem, temos aí um cilindro sem tampa que será mais ou menos assim:
O volume do cilindro será:
O cilindro mais leve será aquele que usa menos material e que, portanto, tem a menor área:
Passo 2
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Não dá para otimizar a função área que a gente tem, pois há duas variáveis. Temos que relacionar uma com a outra antes. Para isso, usamos a expressão do volume:
Substituindo:
Passo 3
Derivamos essa função e achamos os pontos críticos.
Agora derivamos para achar os pontos críticos:
Temos pontos críticos quando a derivada não existe ou é zero.
Ela não vai existir quando , nesse ponto, porém, a área será zero, então a gente esquece isso aí.
A derivada é zero para:
Passo 4
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Vamos ver se esse é um ponto de mínimo mesmo. Um valor à esquerda é e à direita .
Como a derivada é negativa à esquerda e positiva à direita, temos um ponto de mínimo.
Passo 5
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Não temos outros pontos críticos a considerar aqui, então, próximo passo!
Passo 6
Pegamos o melhor ponto crítico obtido no passo e comparamos com os valores na fronteira da função. O melhor valor de todos será o valor ótimo.
O menor valor possível para r é zero. Vimos que nesse valor, a área será nula. Então não consideramos.
O maior valor possível é . Assim:
Dessa maneira, o ponto de mínimo encontrado é global.
Quando tem esse valor:
Resposta
Exercício Resolvido #9
George B.Thomas, Cálculo Volume 1, 11ª ed. São Paulo: Pearson Education do Brasil Ltda, 2009, pp. 311-12. MODIFICADO
Determine o volume do maior cone de revolução que pode ser inscrito em uma esfera de raio .
Passo 1
Deve-se desenhar o problema e anotar as condições dadas, o que é super importante para um melhor entendimento do problema.
O volume do cone estará limitado pelo volume da esfera. A chave para resolvê-lo é relacionar as variáveis dos dois. O volume da esfera será:
O volume do cone, de acordo com as dimensões da figura:
Passo 2
Analisando as equações, chegamos na função que desejamos otimizar em função de apenas uma variável.
Para isso, devemos relacionar e . Olhando a figura, vemos que:
Agora é substituir:
Passo 3
Derivamos essa função e achamos os pontos críticos.
Agora derivamos para achar os pontos críticos:
Os pontos críticos estão onde a derivada não existe ou é zero. Sempre vai existir pois é um polinômio. Vai ser zero quando:
As raízes serão e . Não consideramos o valor negativo, pois é uma medida. Vamos ver o ponto então.
Passo 4
Analisamos os sinais das derivadas antes e depois dos pontos críticos para garantir que sejam máximo ou mínimo.
Vamos ver se esse é um ponto de máximo mesmo. Um valor à esquerda é e à direita .
Como a derivada é positiva à esquerda e negativa à direita, temos um ponto de máximo.
Passo 5
Caso achemos mais de um ponto crítico, temos que testá-los na função para ver qual deles é melhor (que dá um valor de máximo maior ou um valor de mínimo menor).
Não temos outros pontos críticos a considerar aqui, então, próximo passo!
Passo 6
Pegamos o melhor ponto crítico obtido no passo e comparamos com os valores na fronteira da função. O melhor valor de todos será o valor ótimo.
O menor valor possível para é zero. Nesse valor, o volume será nulo. Então não consideramos.
O maior valor possível é , que é o raio da esfera. Assim:
Esse também deu zero, então não precisamos nos preocupar com ele.
Para o nosso ponto de máximo:
Comparando com os outros valores, vemos que é um ponto de máximo global.