Otimização – Modelagem
Teoria
Modelagem algébrica no plano cartesiano
O lado esquerdo do retângulo abaixo está sobre o eixo , ou seja, tem coordenada . O lado direito está limitado pela curva , ou seja, está inscrito nessa curva.
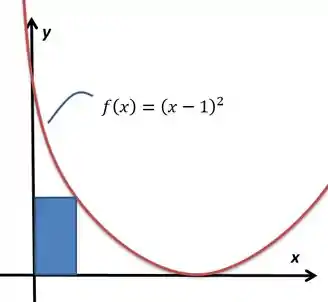
Como a gente poderia maximizar essa área? Que tipo de otimização trabalhamos aqui?
Modelar algo algebricamente é atribuir variáveis a algumas medidas, como , etc.
Foi exatamente isso que fizemos até agora. Modelagem algébrica no plano cartesiano, porém, é atribuir variáveis a algumas medidas no plano cartesiano. Como, por exemplo:
O lado esquerdo do retângulo abaixo está sobre o eixo , ou seja, tem coordenada . O lado esquerdo está limitado pela curva , ou seja, está inscrito nessa curva.
Modelar algebricamente no plano cartesiano é, por exemplo, substituir as medidas desse retângulo pelas variáveis do plano . Como o lado direito está limitado por , sua altura será:
A base será o próprio . A área desse retângulo será:
Otimizar essa área agora seria fácil. Só encontrar os pontos críticos derivando e igualando a zero e depois mostrar que é máximo ou mínimo.
Problemas com ângulos
Alguns problemas de otimização que envolvem ângulos, costumam requerer o conhecimento de relações trigonométricas pra resolver. Como gostamos muito de você, fique atento:
Se a gente dividir tudo por :
Ou por :
As somas de ângulos também são importantes:
Onde:
Vamos aplicar nos exercícios de fixação?
Problemas com ângulos
Exercícios Resolvidos
Exercício Resolvido #1
UFF - Cálculo IA - Lista 16 – 9
Um quadro de altura está pendurado em uma parede vertical de modo que sua borda inferior está a uma altura do raio de visão horizontal de um observador. A que distância da parede deve colocar-se o observador para que a sua posição seja a mais vantajosa para contemplar o quadro, isto é, para que o ângulo de visão seja máximo?
Passo 1
Agora que chegamos até aqui, vamos diluir os passos e ser mais diretos na resolução.
Vou esboçar então o que a questão pede, onde o pedaço em vermelho é o quadro e em laranja essa distância ao chão, com o ângulo de nome .
Passo 2
Olha o que dá para dizer se eu chamar aquele ângulo de visão da parte inferior do quadro com a horizontal de e a distância da pessoa que vê o quadro horizontalmente ao quadro de .
Não sei se você vai lembrar, mas existe uma fórmula relacionando soma de tangentes. É essa aqui:
Se eu somar as tangentes de e de eu vou achar uma expressão que me trará a cara da tangente de . Tendo ela posso procurar um meio de otimizar esse .
Passo 3
Vamos lembrar uma coisa, a questão pede para encontrarmos a distância que gera o maior ângulo de visão. Logo, é como se tivéssemos que achar um e, a partir dele, descobrir em o que gera o maior . Enfim, podemos fazer isso implicitamente, já no formato que está aqui em cima, com o detalhe que deve ser no ponto em questão.
Essa é a nossa distância, em termos das alturas!
Resposta
Exercício Resolvido #2
UFF - Cálculo IA - Lista 16 – 8
Se um objeto dista unidades de um foco de intensidade luminosa constante , a luminosidade do objeto é igual a . Dois focos, e com intensidades e , respectivamente, encontram-se separados por unidades. Em que ponto do segmento de reta liga a , a luminosidade é mínima? Qual deve ser a razão entre e para que o ponto de luminosidade mínima entre os dois focos esteja a uma distância de unidades da fonte de luminosidade ?
Passo 1
Bom, se imaginarmos que a intensidade luminosa num ponto é igual a soma de toda intensidade incidente nela teremos que a intensidade num ponto qualquer entre será:
Esquematizando a figura, teríamos algo assim:
Onde, pelo enunciado:
Assim, a intensidade num ponto qualquer da reta que une as duas fontes será:
Para minimizarmos essa função devemos derivá-la e igualar a .
Passo 2
Esse é o onde a intensidade é mínima. Para provar que ele é realmente de mínimo e não máximo basta analisar que nas proximidades das lâmpadas a intensidade tende a .
Passo 3
Quanto a segunda pergunta, basta igualar esse achado a e achar a relação entre e que é gerada:
Resposta
Exercício Resolvido #3
PUC-RJ - Cálculo 1 - P2 2010.2 – 3
Dentre os retângulos limitados pelo eixo , pelo eixo e pelo gráfico de definida por (conforme a figura), determine as dimensões do retângulo de área máxima.
Passo 1
Bom, a área desse retângulo é dada pela base vezes a altura. No caso, a base é a distância horizontal entre o ponto do gráfico e o eixo , que acaba sendo mesmo. Já a altura é dada por , o que nos faz concluir que a área é dada por:
Passo 2
Para otimizá-la vamos derivar a área em função de e igualar o termo a . Como é um polinômio, ela vai sempre existir.
Por Bhaskara, temos que as raízes serão:
Como vemos, ao substituir na função teríamos uma área nula:
Para saber se é um ponto de máximo mesmo, devemos testar o sinal da derivada. Como é fácil de derivar, podemos usar o teste da segunda derivada.
Como a segunda derivada é negativa no ponto crítico, podemos concluir que o responsável pelo retângulo de área máxima é .
É um ponto de máximo global, pois no outro ponto crítico, que a fronteira direita, a área é nula. No ponto , que é a fronteira à esquerda:
Uma vez que é a base do retângulo e a sua altura, descobrimos:
Essas são as dimensões do nosso retângulo, !
Resposta
Exercício Resolvido #4
PUC-RJ - Cálculo 1 - P2 2012.1 - 3
Um triângulo retângulo, localizado no primeiro quadrante, tem um vértice na origem e seus outros dois vértices determinados pela interseção da reta tangente ao gráfico da função com os eixos coordenados (ver figura).
Determine a equação da reta tangente ao gráfico da em .
Determine as interseções da reta com o eixo e com o eixo .
Determine o valor de de forma que a área do triângulo seja máxima, considerando somente os triângulos formados no quadrante.
Passo 1
Vamos modelar uma reta , (não usei para não confundir com o ). Sabemos que seu coeficiente angular é igual a em .
Sabemos ainda, porém, que a função da reta passa pelo ponto quando , ou seja, passa pelo ponto . Assim descobrimos o :
Enfim, concluímos a nossa reta:
Passo 2
Suas interseções com os eixos e acontecem em e respectivamente:
Passo 3
Pela figura inicial percebemos que o triângulo tem como dimensões de altura e base as interseções com os eixos e , respectivamente. Logo, sua área será:
Para achar a área máxima devemos derivar a função em relação a e igualar a expressão a . Ela vai sempre existir, pois a o denominador é sempre maior que zero.
Como o triângulo deve ser formado no primeiro quadrante, é o único valor que nos serve. A gente observa que e , o que garante que é ponto de máximo e não mínimo, dado que é o único máximo em .