Exercícios de Otimização – Casos Clássicos - Lista de Exercícios Resolvida
Questão 1
Determine o volume do maior cone de revolução que pode ser inscrito em uma esfera de raio .
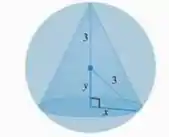
Questão 2
Encontre as dimensões do retângulo com a maior área que pode ser inscrito em um triângulo equilátero com lado se um dos lados do retângulo estiver sobre a base do triângulo.
Ver solução completaQuestão 3
Seja uma reta passando pelo ponto com inclinação negativa. Dentre todos os triângulos retângulos obtidos tomando e a interseção da reta com o primeiro quadrante, encontre as dimensões do que possui a menor hipotenusa.
Ver solução completaQuestão 4
Um campo retangular à margem de um rio deve ser cercado com exceção do lado ao longo do rio. Se o custo do material for de no lado paralelo ao rio e de nos dois extremos, ache o campo de maior área que possa ser cercado com de materiais.
Ver solução completaQuestão 5
Quais são as dimensões da mais leve lata em forma de cilindro reto, sem tampa, para conter exatamente .
Ver solução completaQuestão 6
Encontre as dimensões de um retângulo com um perímetro de cuja área seja a maior possível.
Ver solução completaQuestão 7
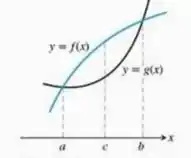
Sejam e as funções deriváveis traçadas aqui. O ponto é onde a distância vertical entre as curvas é máxima. Há algo de especial em relação às tangentes às duas curvas em ? Justifique sua resposta.
Questão 8
Uma cerca de de altura corre paralela a um edifício alto a uma distância de do edifício. Qual o comprimento da menor escada que se apoie no chão e na parede do prédio por cima da cerca?
Ver solução completaQuestão 10
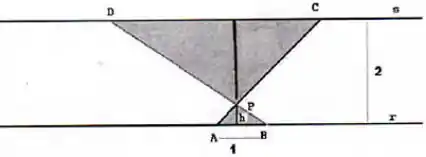
Na figura abaixo, e são retas paralelas, a distância entre elas é , é um ponto fixo de , e são pontos fixos de e a distância entre eles é . É possível encontrar um ponto na reta , de modo que o segmento intercepte e que a soma das áreas dos triângulos sombreados na figura seja mínima? E máxima? Nos casos em que a resposta for afirmativa, encontre a altura do triângulo .
Questão 11
Um edifício com base retangular de deve ser construído num lote com lados paralelos ao do edifício, sendo exigido recuos de na frente e no fundo, e recuos de nas laterais. Ache as dimensões do lote com menor área onde esse edifício pode ser construído.
Ver solução completaQuestão 12
Quais são as dimensões do retângulo de maior área que pode ser inscrito em um semicírculo de raio ?
Ver solução completaQuestão 13
Um fazendeiro tem pés de cerca e quer cercar um campo retangular que está na margem de um rio reto. Ele não precisa cercar ao longo do rio. Quais são as dimensões do campo que tem a maior área?
(a) por
(b) por
(c) por
(d) por
(e) por
Ver solução completaQuestão 14
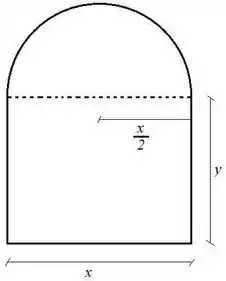
Uma janela é construída com um semicírculo e um retângulo como na figura abaixo. Sabendo que seu perímetro é , determine as dimensões da janela para que sua área seja máxima.
Questão 15
Seja uma reta que passa pelo ponto e forma um triângulo com os eixos coordenados positivos. Determine a equação de para que área desse triângulo seja mínima.
Ver solução completaQuestão 16
Seja uma reta passando pelo ponto com inclinação negativa. Dentre todos os triângulos retângulos obtidos tomando e a interseção da reta com o primeiro quadrante, encontre as dimensões do que possui a menor hipotenusa.
Ver solução completaQuestão 17
As margens de cima e de baixo de um pôster tem e as margens laterais medem cada. Se a área do material impresso sobre o pôster estiver fixa em , encontre as dimensões do pôster com a menor área.
Ver solução completaQuestão 19
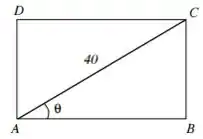
A superfície lateral de um cilindro reto é obtida unindo-se os lados e de um retângulo . Dentre todos os retângulos de diagonal , determine o ângulo (ver figura) que permite construir um cilindro de volume máximo.
Questão 20
Um fabricante de latas precisa fabricar latas cilíndricas com capacidade de 1 L. Sabendo que o custo do material da tampa é o dobro do custo da parte lateral e do fundo, qual as dimensões da lata que proporciona o custo mínimo.
Ver solução completaQuestão 21
(a) Mostre que, de todos os retângulos com perímetro , aquele com maior área é o quadrado. (b) Mostre que de todos os retângulos com área A, o de menor perímetro é o quadrado.
Ver solução completaQuestão 24
Considere todos os retângulos inscritos na semi-elipse de equação , com , e que possuem um de seus lados sobre o eixo .
- Determine uma função que expresse a área destes retângulos, bem como seu domínio.
- Ache as dimensões do retângulo de maior área.
Questão 25
Uma janela normanda tem a forma de um retângulo tendo em cima um semicírculo, cujo diâmetro é igual à largura do retângulo. Suponha que o perímetro da janela normanda é de .
- Escreva a área da janela como função da altura do retângulo correspondente.
- Aplicando os métodos do cálculo diferencial na função do item (a), ache as dimensões da janela com maior área possível, assim como a área desta janela.
Questão 26
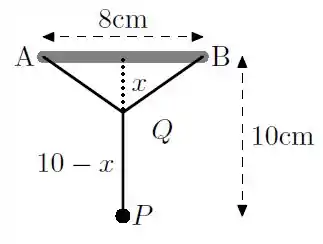
Um peso deve ser mantido suspenso a de uma barra horizontal de extremidades e , por um fio na forma de (veja na figura). Sabendo que o segmento mede , qual o fio de menor comprimento que pode ser usado?
Questão 27
Sejam e pontos contidos no eixo e eixo , respectivamente, tais que o segmento ligando e passa por . Determine e tal que a área do triângulo com vértices e é mínima.
Ver solução completaQuestão 28
Um rio tem de largura. Deseja-se estender um cabo de comunicação ligando os pontos e , situados em margens opostas. O ponto está a justante (isto é, rio abaixo) do ponto , conforme a figura.
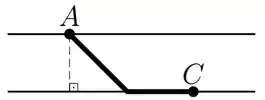
O custo de instalação do cabo é de por metro no leito do rio e de por metro no solo seco. Determine quantos metros de cabo deverão ser instalados no rio e quantos em terra para que o custo total seja mínimo.
Ver solução completaQuestão 29
3) Determine o maior volume possível que pode conter uma caixa (paralelepípedo) com base quadrada, construída com de material, e que não inclui a tampa.
Ver solução completaQuestão 30
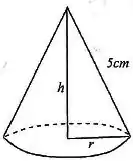
Determine as dimensões de um cone circular reto de maior volume cuja geratriz tenha de comprimento.
Questão 31
3. Considere a família de todos os triângulos retângulos como na figura abaixo. Um vértice do triângulo é a origem do plano e a hipotenusa é o segmento de reta tangente ao gráfico da função .
a) Existe um triângulo com área máxima? Justifique sua resposta.
b) Encontre o comprimento da menor hipotenusa desta família de retângulos. Justifique sua resposta.
Ver solução completaQuestão 32
Uma caixa sem tampa, de base quadrada, deve ser construída de forma que seu volume seja . O material da base vai custar por e o material dos lados por . Encontre as dimensões da caixa de modo que o custo do material seja mínimo
Ver solução completaQuestão 33
Uma casa tem uma janela em forma de arco cujo formato é dado pela metade superior de uma elipse. A casa será reformada e deseja-se colocar concreto no arco a fim de fechá-lo, mantendo-se apenas uma janela retangular, como na figura abaixo:
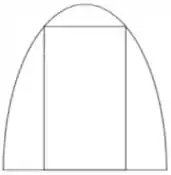
Considerando que o arco original tem altura igual a e largura igual a , qual o maior valor possível para a área dessa janela?
Ver solução completaQuestão 34
Um cilindro circular reto é inscrito em uma esfera de raio . Encontre a maior área de superfície possível para esse cilindro.
Ver solução completaQuestão 35
Dentre todos os triângulos isósceles de perímetro conhecido, determine aquele que possui a maior área.
Ver solução completaQuestão 36
Um caixa de água no formato de um prisma reto, cuja base é um triângulo equilátero, deverá ser construída e conter de capacidade. Calcule as dimensões desta caixa, de modo que a área total seja mínima
Ver solução completaQuestão 37
4. Um terreno retangular deve ser cercado. Dois lados opostos devem receber uma cerca reforçada que custa o metro, enquanto os outros dois restantes recebem uma cerca padrão de o metro. Quais são as dimensões do terreno de maior área que pode ser cercado com ?
Ver solução completaQuestão 38
Encontre as dimensões do cone circular de maior volume que pode ser inscrito em uma esfera de raio . Calcule o volume desse cone.
Ver solução completaQuestão 39
Um publicitário está planejando um cartaz retangular que deve ter margens de cm na parte superior e nos lados e uma margem de cm na parte inferior. Por medida de economia, a área total do cartaz deve ser a menor possível, mas a área impressa deve ter cm²: Quais devem ser as dimensões do cartaz? Justifique sua resposta!
Ver solução completaQuestão 40
Um retângulo deve ser circunscrito em uma semicircunferência de raio 5 metros. Qual é a maior área que o retângulo pode ter e quais as suas dimensões?
Ver solução completaQuestão 41
Uma refinaria de petróleo está em na margem norte de um rio reto que tem de largura. Um oleoduto deve ser construído da refinaria até um tanque de armazenamento em na margem sul do rio, a leste da refinaria. O custo de construção do oleoduto é sobre a terra, até um ponto na margem norte do rio é sob o rio até o tanque.
a) Obtenha o custo total de construção do oleoduto, , em função da distância , entre e .
b) Determine os pontos críticos de em .
c) Qual o valor de que minimiza o custo de construção do oleoduto?
Ver solução completaQuestão 42
Considere um cone circular reto de altura e raio . Dentre os cilindros circulares retos que podem ser inscritos nesse cone (conforme figura abaixo), determine a altura do cilindro que tem volume máximo.
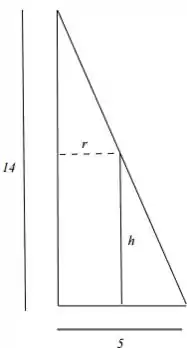
Questão 43
Considere todos os triângulos retângulos formados pelos semieixos positivos e por uma reta que passa pelo ponto (2,3). Dentre todos os triângulos possíveis, aquele que possui área mínima tem a hipotenusa valendo:
Ver solução completaQuestão 44
Seja um ponto da curva mais próximo do ponto . A distância entre e é:
- .
- .
- .
- .
Questão 45
Quando um prato circular de metal é aquecido em um forno, seu raio aumenta a uma taxa (isto é, a derivada do raio com relação ao tempo) de . Qual é a derivada da área do prato quando seu raio é ?
Ver solução completaQuestão 47
Se de material estiverem disponíveis para fazer uma caixa com uma base quadrada e sem tampa, encontre o maior volume possível da caixa.
(a)
(b)
(c) Nenhume das alternativas
(d)
(e)
Ver solução completaQuestão 48
Dentre todos os triângulos isósceles circunscritos a um círculo de raio existe um cuja área é máxima? E mínima? Se sim, qual é essa área? Justifique.
Ver solução completaQuestão 49
Considere a parábola .
- Encontre uma expressão para a distância de um ponto pertencente à parábola até o ponto .
- Determine o(s) ponto(s) da parábola no(s) qual(is) a distância ao ponto seja mínima.
Questão 50
Dentre todos os retângulos do plano com centro na origem, lados paralelos aos eixos coordenados e inscritos na elipse
determine aquele de maior perímetro.
Ver solução completaQuestão 51
Encontre as dimensões do cone circular de maior volume que pode ser inscrito em uma esfera de raio . Calcule o volume desse cone.
Ver solução completaQuestão 52
Para produzir uma caixa com base quadrada são usados materiais cujos custos são os seguintes: 1 real por metro quadrado para a base, e 4 reais por metro quadrado para as laterais. Quais devem ser as dimensões da caixa, sem tampa, que suporta 1 metro cúbico de volume, que minimizam o custo da caixa?
Ver solução completaQuestão 53
Se é o ponto na curva que está mais próximo de então é:
- nenhuma das alternativas
Questão 54
Um pedaço de fio com de comprimento é cortado em duas partes. Uma parte é dobrada no formato de um quadrado, ao passo que a outra é dobrada na forma de um triângulo equilátero. Como deve ser cortado o fio de forma que a área total englobada seja: (a) máxima? (b) mínima?
Ver solução completa