Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Comprimento de Arco

Ver Todos os Exercícios

Teoria

Como Calcular?

Imagine que temos uma curva σ t = x t , y t , z t . Queremos saber qual é o comprimento de um arco, ou seja, qual o comprimento de uma parte dessa curva. Como fazer?

Relaxa, é super tranquilo. Para calcular o comprimento de um arco de σ ( t ) , do ponto σ ( t 1 ) ao ponto σ ( t 2 ) , basta usar a seguinte fórmula:

L = ∫ t 1 t 2 σ ' ( t ) d t

Onde

σ ' ( t ) = x ' t 2 + y ' t 2 + z ' t 2

Agora, pra ficar mais fácil ainda, vou te dar aquele passo-a-passo que eu sei que você gosta:

  1. Encontrar t 1 e t 2 .
  2. Calcular σ ' ( t ) .
  3. Calcular σ ' t .
  4. Substituir em L .

Exemplo:

Calcule o comprimento da seguinte curva:

σ t = ( 2 cos ⁡ t , 2 sen ⁡ t )

0 ≤   t < 2 π

  1. Encontrar t 1 e t 2 :

    2. Queremos calcular o comprimento da curva do ponto σ ( 0 ) ao ponto σ ( 2 π ) :

    t 1 = 0 t 2 = 2 π

  2. Calcular σ ' ( t ) :

    3. σ ' t = ( - 2 sen ⁡ t , 2 cos ⁡ t )

  3. Calcular σ ' ( t ) :

    4. σ ' ( t ) = - 2 sen ⁡ t 2 + 2 cos ⁡ t 2 = 2

  4. Substituir em L :

L = ∫ t 1 t 2 σ ' ( t ) d t = ∫ 0 2 π 2   d t = 2 ∫ 0 2 π d t = 4 π

Esse resultado te parece familiar? Talvez você tenha notado que a curva σ ( t ) é um círculo de raio r = 2 , certo? Então olha que maneiro: encontramos o resultado certinho do comprimento do círculo. Isso mostra que a fórmula funciona de verdade!

Então mãos à obra e partiu exercícios!

Exercícios Resolvidos

Exercício Resolvido #1

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p 33 – exercício 1 letra d

Encontre o comprimento do caminho percorrido por uma partícula que se move ao longo da curva de equação dada durante o intervalo de tempo especificado:

σ t = t ,   3 t 2 ,   6 t 3 ,     0 ≤ t ≤ 2

Passo 1

L = ∫ t 1 t 2 σ ( t )   d t

Encontrar t 1 e t 2 :

O problema já forneceu os valores de t 1 e t 2 .

Portanto:

t 1 = 0 t 2 = 2

Passo 2

Calcular σ ' ( t ) :

σ ' t = 1 ,   6 t , 18 t 2

Passo 3

Calcular σ ' ( t ) :

σ ' ( t ) = 1 2 + 6 t 2 + 18 t 2 2

σ ' ( t ) = 18 2 t 4 + 36 t 2 + 1

Note que essa expressão tá com cheiro de quadrado perfeito: a 2 + 2 a b + b 2

Comparando termo a termo:

a 2 = 18 2 t 4 2 a b = 36 t 2 b 2 = 1

Resolvendo esse sistema, encontramos que:

a = 18 t 2   b = 1

Logo:

a 2 + 2 a b + b 2 = a + b 2

⇒ 18 2 t 4 + 36 t 2 + 1 = 18 t 2 + 1 2

Substituindo acima temos que:

σ ' ( t ) = 18 t 2 + 1 2

σ ' ( t ) = 18 t 2 + 1

Passo 4

Substituir em L :

L = ∫ t 1 t 2 σ ' ( t )   d t

⇒ L = ∫ 0 2 18 t 2 + 1   d t

Calculemos então a integral indefinida:

∫ 18 t 2 + 1   d t = 6 t 3 + t

Substituindo na integral definida:

L = 6 2 3 + 2 - 6 0 3 + 0

⇒ L = 50 - 0

⇒ L = 50

Resposta

L = 50

Exercício Resolvido #2

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p.33. questão 2.

Uma curva tem equação y 2 = x ³ . Encontre o comprimento da curva do ponto ( 1 , - 1 ) ao ponto ( 1,1 ) .

Passo 1

Bom, essa curva não está parametrizada. Então, devemos parametrizá-la. Para isso, observe que

x = y 2 3

Podemos então usar a parametrização natural, fazendo:

y t = t

x t = t 2 3

Agora temos a curva

σ t = t 2 3 , t

Passo 2

Precisamos encontrar ainda t 1 e t 2 . Observe que a questão pede o comprimento do ponto ( 1 , - 1 ) ao ponto ( 1,1 ) . Então, em t 1 a curva está no ponto ( 1 , - 1 ) e em t 2 , esta no ponto ( 1,1 ) . Então

t 1 2 3 = 1

t 1 = - 1

E

t 2 2 3 = 1

t 2 = 1

Passo 3

Agora vamos calcular σ ' ( t ) :

σ t = t 2 3 , t

σ ' t = 2 3 t - 1 3 , 1

σ ' ( t ) = 2 3 t - 1 3 2 + 1 2 = 4 9 t - 2 3 + 1

- ''

Passo 4

Pronto, agora só substituir na fórmula

L = ∫ t 1 t 2 σ ' ( t )   d t

L = ∫ - 1 1 4 9 t - 2 3 + 1   d t = ∫ - 1 1 4 + 9 t 2 3 9 t 2 3   d t = ∫ - 1 1 4 + 9 t 2 3 3 t 1 3   d t

L = 1 3 ∫ - 1 1 4 + 9 t 2 3 t 1 3   d t = 1 3 ∫ - 1 0 - 4 + 9 t 2 3 t 1 3   d t + ∫ 0 1 4 + 9 t 2 3 t 1 3   d t

L = 1 3 ∫ - 1 0 - 4 + 9 t 2 3 t 1 3   d t + ∫ 0 1 4 + 9 t 2 3 t 1 3   d t

L = 1 3 ( - 1 9 4 + 9 t 2 3 3 2 0 - 1 + 1 9 4 + 9 t 2 3 3 2 1 0

L = 1 3 . 1 9 4 + 9 t 2 3 3 2 1 0 - 4 + 9 t 2 3 3 2 0 - 1

L = 1 27 13 13 - 64 - 64 - 13 13 = 1 27 2.13 13 - 2.8

L = 2 27 13 13 - 8

Resposta

L = 2 27 13 13 - 8

Exercício Resolvido #3

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p.34. questão 7.

Uma curva C é a união de duas curvas C 1 e C 2 , onde C 1 é um segmento de reta e C 2 é uma porção da circunferência, conforme a figura. Pede-se:

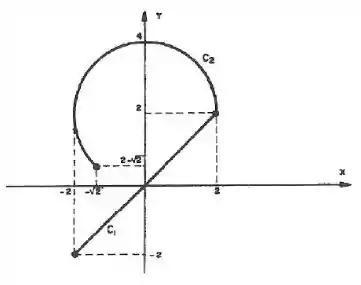
  1. Parametrize curvas C 1 e C 2
  2. O comprimento total de C .

Passo 1

C 1 é um segmento de reta.

Se observarmos a figura vemos que os pontos ( 2,2 ) , ( 0,0 ) e ( - 2 , - 2 ) pertencem ao segmento. Assim, esse segmento nada mais que é que a reta x = y , com t ∈ [ - 2,2 ] :

σ C 1 t = t , t ,   - 2 ≤ t ≤ 2

Passo 2

Já C 2 é uma porção da circunferência de raio r = 2 , centrada em ( 0,2 ) .

A parametrização da circunferência nós já conhecemos. Assim:

σ C 2 t = ( 2 cos ⁡ t ,   2 s e n   t + 2 )

Passo 3

Mas, precisamos notar que C 2 é apenas uma porção da circunferência, portanto, precisamos descobrir os limites do parâmetro t .

Para isso, observamos que,no ínicio da curva ( t = t 1 ) , temos o ponto ( 2,2 ) e no final da curva ( t = t 2 ) , temos o ponto ( - 2 , 2 - 2 ) . Assim:

2 cos ⁡ t 1 ,   2 s e n   t 1 + 2 = 2,2

2 cos ⁡ t 1 = 2

2 s e n   t 1 + 2 = 2

Então:

t 1 = 0

E

2 cos ⁡ t 2 ,   2 s e n   t 2 + 2 = ( - 2 , 2 - 2 )

2 cos ⁡ t 2 = - 2

2 s e n   t 2 + 2 = 2 - 2

Então:

t 2 = arccos ⁡ - 2 2

t 2 = a r c s e n - 2 2  

Assim:

t 2 = 5 π 4

Então, a parametrização de C 2 é:

σ C 2 t = 2 cos ⁡ t ,   2 s e n   t + 2 ,   0 ≤ t ≤ 5 π 4

Passo 4

Agora precisamos observar que C = C 1 + C 2 , então, para calcular o comprimento total de C , basta calcularmos o comprimento de C 1 e de C 2 e depois somar os dois.

Começando por C 1 :

σ C 1 t = t , t

σ C 1 ' t = 1,1

σ C 1 ' ( t ) = 1 2 + 1 2 = 2

Passo 5

Agora C 2 :

σ C 2 t = 2 cos ⁡ t ,   2 s e n   t + 2

σ C 2 ' t = - 2 sen ⁡ t ,   2 c o s   t

σ C 2 ' t = - 2 sen ⁡ t 2 + 2 cos ⁡ t 2 = 4 = 2

Passo 6

Para calcular os comprimentos precisamos apenas substituir nossos resultados em

L = ∫ t 1 t 2 σ ' ( t ) d t

Assim,

L C 1 = ∫ - 2 2 σ C 1 ' t d t = ∫ - 2 2 2 d t = 2 t 2 - 2 = 2 2 - - 2 = 4 2  

E

L C 2 = ∫ 0 5 π 4 σ C 2 ' t d t =   ∫ 0 5 π 4 2 d t = 2 t 5 π 4 0 = 2 5 π 4 - 0 = 5 π 2

Passo 7

O comprimento da curva C é, portanto:

L C = L C 1 + L C 2 = 4 2 + 5 π 2 = 8 2 + 5 π 2

Resposta

σ C 1 t = t , t ,   - 2 ≤ t ≤ 2

σ C 2 t = ( 2 cos ⁡ t ,   2 s e n   t + 2 )

L C = 8 2 + 5 π 2

Exercício Resolvido #4

UFRJ, Cálculo Diferencial e Integral 2, P1 2014.2, questão múltipla escolha 5

Uma partícula se move numa hélice com vetor posição no tempo t , r t = cos ⁡ t , sen ⁡ t ,   2 t ,     t ≥ 0 . Qual é o tempo para que a distância percorrida seja 3 π ?

(a) 3 π 2

(b) 3 5 π

(c) 3 π 5

(d) 6 π

(e) 3 π

Passo 1

Queremos o tempo para que a distância percorrida seja 3 π , certo? Mas essa distância nada mais é que o comprimento de arco da hélice do tempo inicial t = 0 até o tempo que procuramos, que podemos chamar de t 1 .

Portanto, pela fórmula do comprimento de arco:

∫ 0 t 1 r ' ( t ) d t = 3 π

Passo 2

Vamos calcular r ' ( t ) :

r t = cos ⁡ t , sen ⁡ t ,   2 t

⇒ r ' t = - sen ⁡ t , cos ⁡ t , 2

Então o módulo de r ' ( t ) é:

r ' ( t ) = - sen ⁡ t 2 + cos 2 ⁡ t + 2 2

⇒   r ' ( t ) = sen 2 ⁡ t + cos 2 ⁡ t + 4

⇒   r ' ( t ) = 5

Passo 3

Show! Voltando à fórmula do comprimento de arco:

∫ 0 t 1 r ' ( t ) d t = 3 π

⇒   ∫ 0 t 1 5 d t = 3 π

⇒ 5 t 0 t 1 = 3 π

⇒ 5 t 1 = 3 π

⇒ t 1 = 3 π 5

Resposta

Alternativa (c)

Exercício Resolvido #5

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, p.33. questão 5.

Uma partícula se move ao longo de uma curva definida por

σ t = t - s e n   t ,   1 - cos ⁡ t ,   0 ≤ t ≤ 2 π

  1. Determine os instantes t 1 e t 2 ∈ [ 0,2 π ] em que v t = 1 .
  2. Calcule o espaço percorrido pela partícula no intervalo de tempo [ t 1 , t 2 ] .

Passo 1

a )

Calculando v ( t ) :

v t = σ ' t = ( 1 - cos ⁡ t , s e n   t )

Passo 2

Para saber em que instantes v t = 1 precisamos calcular a velocidade escalar da partícula e igualar a 1.

v t = 1 - cos ⁡ t 2 + s e n   t 2 = 1 - 2 cos ⁡ t + c o s 2 t + s e n 2 t = 2 - 2 cos ⁡ t

Passo 3

Igualando a 1:

2 - 2 cos ⁡ t = 1

2 - 2 cos ⁡ t = 1 2 = 1

- 2 cos ⁡ t = - 1

cos ⁡ t   = 1 2

t = n π 3

Mas, como t ∈ [ 0,2 π ] :

t 1 = π 3

t 2 = 5 π 3

Passo 4

b )

Para achar o espaço percorrido pela partícula, basta calcularmos o comprimento da curva que modela a trajetória da partícula.

L = ∫ t 1 t 2 σ ' ( t ) d t

σ ' ( t ) = v t = 2 - 2 cos ⁡ t

t 1 = π 3

t 2 = 5 π 3

Passo 5

Substituindo nossos dados na fórmula e desenvolvendo as contas:

L = ∫ π 3 5 π 3 2 - 2 cos ⁡ t d t = 4 3

Resposta

  1. t 1 = π 3 e t 2 = 5 π 3
  2. L = 4 3

Exercícios de Livros Relacionados

(a) Trace a epitrocoide com equações x = 11 cos ⁡ t - 4 cos ⁡ 11 t 2 y = 11 sen ⁡ t - 4 sen ⁡ 11 t 2 Qual intervalo do parâmetro fornece a curva completa?b) Use seu SCA para calcular o comprimento apr
Um barbante é enrolado ao redor de um círculo e então desenrolado, sendo mantido esticado. A curva traçada pelo ponto P no final do barbante é chamada involuta do círculo. Se o círculo tiver raio r e
Calcule o comprimento exato da curva polar: r = 2 c o s θ 0 ≤ θ ≤ π
51-54. Use uma calculadora ou um computador para encontrar o comprimento do laço, com precisão de quatro casas decimais. Se necessário, use um gráfico para determinar o intervalo de parâmetro.53. r =
Ao gravar apresentações ao vivo, os engenheiros de som usam um padrão de captação em forma de cardioide, pois ele suprime o barulho da audiência. Suponha que o microfone esteja colocado a 4m da frente