Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 55
(a) Trace a epitrocoide com equações
Qual intervalo do parâmetro fornece a curva completa?
b) Use seu SCA para calcular o comprimento aproximado dessa curva.
Passo 1
Fala ai galerinha. De boa? Preparado para traçar uma curva parametrizada por e e calcular o comprimento dessa curva?
Vamos entender um pouco como faremos isso? Se liga! 😊
Para resolver o problema
- Na letra A, vamos traçar a curva epitrocoide no plano cartesiano utilizando a parametrização dada, é claro que vamos utilizar um software e identificar o intervalo da curva completa.
- Na letra B, vamos utilizar a fórmula do comprimento de arco para curvas parametrizadas:
- Calculamos as derivadas e e substituímos na fórmula.
- Simplificamos a expressão resultante e integramos numericamente no intervalo encontrado, obtendo o comprimento aproximado.
.
Agora é só resolver, Bora!
Passo 2
Show de bola, galera....Parece complicado, mas vamos resolver junto!
Vamos esboçar agora o gráfico dessa curva parametrizada por etapas, ou melhor dizendo, por intervalos:
Para
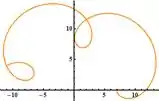
Para
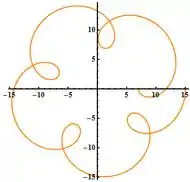
Para
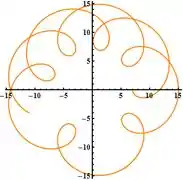
Para
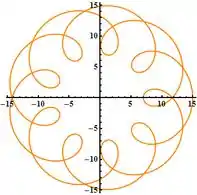
Como podemos observar, o intervalo do parâmetro que fornece a curva completa é:
Passo 3
Aproveitando do nosso recurso computacional, chegamos a um limite de integração para calcular o comprimento aproximado dessa curva:
Passo 4
Agora vamos iniciar derivando as funções em relação a .
Temos
E derivando
Passo 5
Agora podemos substituir as derivadas na formula do comprimento do arco.
Esta integral não tem uma solução analítica simples, portanto, vamos precisar de um recurso computacional.
Prontinho. Chegamos na resposta! Até a próxima! 😉
Resposta
(a)
(b)