Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 44

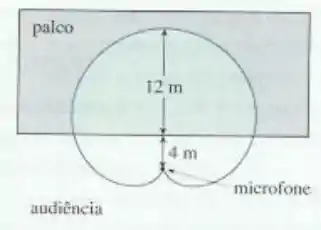
Ao gravar apresentações ao vivo, os engenheiros de som usam um padrão de captação em forma de cardioide, pois ele suprime o barulho da audiência. Suponha que o microfone esteja colocado a 4   m da frente do palco (como na figura) e que o limite da região de captação ótima seja dado pela cardioide r = 8 + 8   s e n   θ , onde r é medido em metros e o microfone está no polo. Os músicos querem saber a área que eles terão no palco dentro da área de captação ótima do microfone. Responda a esta pergunta.

Passo 1

Galera, a área que precisamos calcular é a área de intersecção do palco com o interior da cardioide. Pra isso, precisamos saber em que pontos a cardioide cruza com a fronteira do palco.

Como o polo da cardioide (onde está o microfone) fica na origem do sistema de coordenadas, podemos dizer que a fronteira inferior do palco pode ser representada pela equação:

y = 4

pois está 4   m acima do microfone, conforme a figura do enunciado. Em coordenadas polares, fica assim:

r   s e n   θ = 4

r = 4 s e n   θ

Passo 2

Agora que temos a equação que representa o inferior do palco e a equação do cardioide, podemos igualar r pra descobrir as intersecções:

r = 4 s e n   θ = 8 + 8   s e n   θ

4 = 8   s e n   θ + 8   s e n 2   θ

2   s e n 2   θ + 2   s e n   θ - 1 = 0

s e n   θ = - 2 ± 2 2 - 4   .   2   .   - 1 2   .   2 = - 1 ± 3 2

Como devemos ter - 1 ≤ s e n   θ ≤ 1 , a solução é:

s e n   θ = 3 - 1 2

Então, uma das intersecções equivale a:

θ = a r c s e n 3 - 1 2 ≈ 0,374734   r a d

Passo 3

Show! Agora podemos montar e resolver a integral que nos dá a área procurada, usando a simetria entre os lados direito e esquerdo:

A = 2 ∫ 0,374734 π / 2 1 2 8 + 8   s e n   θ 2 - 4 s e n   θ 2   d θ = ∫ 0,374734 π / 2 64 + 128   s e n   θ + 64   s e n 2   θ - 16 s e n 2   θ   d θ = 16 ∫ 0,374734 π / 2 4 + 8   s e n   θ + 4   s e n 2   θ - 1 s e n 2   θ   d θ = 16 ∫ 0,374734 π / 2 4 + 8   s e n   θ + 4 1 2 - cos ⁡ 2 θ 2 - c o s s e c 2   θ   d θ = 16 ∫ 0,374734 π / 2 6 + 8   s e n   θ - 2 cos ⁡ 2 θ - c o s s e c 2   θ   d θ = 16   6 θ - 8 cos ⁡ θ - s e n 2 θ + c o t g   θ 0,374734 π / 2 ≈ 16 3 π - - 3,33522 ≈ 204,16

Resposta

A ≈ 204,16   m 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reparametrize pelo comprimento de arco a curva γ dada: a )γ t = 2 t + 1,3 t - 1 , t ≥ 0
Reparametrize pelo comprimento de arco a curva γ dada: a )γ t = 2 t + 1,3 t - 1 , t ≥ 0
Seja γ : α ,β → R 2 uma curva dada em coordenadas polares por ρ = ρ θ ,θ ∈ α ,β .(Observação: trata-se da curva dada por x = ρ θ cos ⁡ θ ,y = ρ θ sin ⁡ θ ,θ ∈ α , β ). Supondo que ρ = ρ θ tenha deriva
Calcule o comprimento da curva dada em coordenadas polares (Utilize o exercício 2) a )ρ = θ , θ ∈ 0 , π
Calcule o comprimento da curva dada: a ) γ t = t cos ⁡ t , t sin ⁡ t ,t ∈ 0 ,2 π