Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 45
Calcule o comprimento exato da curva polar:
Passo 1
Fala pessoal. De boa?
Nosso objetivo nessa questão é calcular o comprimento da curva polar definida pela função , onde o parâmetro varia de a .
E como podemos resolver?
- Identificar a função polar
- Derivar a função em relação a
- Usar a fórmula do comprimento de arco polar.
- Simplificamos a expressão resolvendo a integral.
Seguindo esses passos conseguimos a respostas!
Passo 2
Através de um recurso gráfico podemos identificar a nossa curva como:
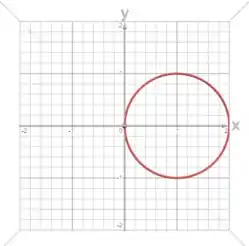
Passo 3
Para encontrarmos o comprimento desejado, devemos lembrar que o comprimento de arco é dado por:
Temos que , logo:
Passo 4
Aplicando na equação do arco, temos:
Lembrando que nosso limite de integração foi fornecido no enunciado
Substituindo os termos, temos
Passo 5
Podemos utilizar outro método para encontrar o comprimento da curva
Uma forma de confirmar tal resultado é notar que a curva é dada em coordenadas cartesianas por:
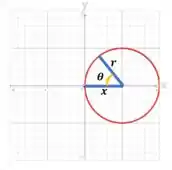
Através do gráfico podemos afirmar que:
Isolando os termos
Lembrando que
Ou seja, completando quadrados:
Dessa forma, temos que a curva é uma circunferência de raio 1, cuja circunferência é .
Resposta
O arco possui comprimento de .