Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 73
Um barbante é enrolado ao redor de um círculo e então desenrolado, sendo mantido esticado. A curva traçada pelo ponto no final do barbante é chamada involuta do círculo. Se o círculo tiver raio e centro , se a posição inicial de for e se o parâmetro for escolhido como na figura, mostre que as equações paramétricas da involuta são
Passo 1
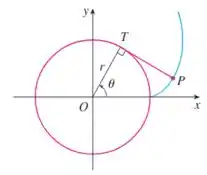
Eaee, belezinha?? Bom... a figura abaixo mostra um barbante esticado (segmento de reta ) fazendo uma tangente com a circunferência de raio e centrada em :
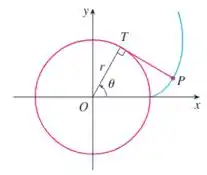
A curva traçada pelo ponto no final do barbante (em azul) é chamada involuta do círculo.
Queremos encontrar as equações paramétricas da curva traçada pelo barbante.
A sacada que precisamos ter aqui é que o comprimento do segmento é apenas a quantidade de barbante desenrolada, que é o comprimento do arco do círculo correspondente ao ângulo .
E que podemos observar que o comprimento desse arco é
Passo 2
Olhando o desenho dado, podemos encontrar as coordenadas de , iniciando com as coordenadas de e subtraindo as componentes horizontal e vertical do segmento .
Inicialmente, o ponto tem coordenadas já que ele está em cima do contorno do nosso círculo. Veja:
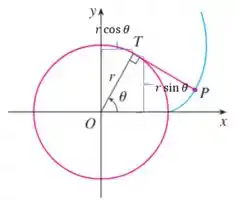
Agora vamos usar um pouquinho nossa imaginação: pense em uma linha horizontal passando pelo ponto .
O ângulo que faz com essa linha horizontal é
Então vamos decompor sua a componente horizontal é . Veja:
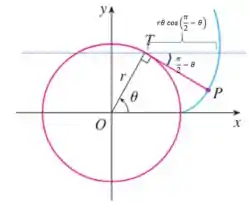
Passo 3
Isto é igual a pois
(Confuso? Vamos dar um exemplo pra ficar melhor de entender: lembra que e ? Perceba que , a situação que temos no nosso problema é mesma desse exemplo: sempre que tivermos dois ângulos cuja soma seja igual a , o cosseno de um será igual ao seno do outro.)
Além disso, a componente vertical de é
Agora, se somarmos e subtrairmos estes dois das coordenadas e (respectivamente) de , obtemos:
Resposta
Demonstração