Equação da Elipse

A equação da elipse, contém muitas variáveis e vai mudar de acordo com a orientação do maior eixo da elipse.

Caso o maior eixo for paralelo ao eixo $x:$

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

Caso o maior eixo for paralelo ao eixo $y:$

$$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$$

Em ambos os casos:

• $a$ é a medida da metade doo eixo maior
• $b$ é a medida da metade do eixo menor
• $xey$ são variáveis da equação

É importante saber que na elipse também existem relações entre o tamanho dos eixos, e a distância do centro até o foco. Se chamamos essa distância de $c$, podemos escrever a relação:

$$a^2=b^2+c^2$$

Para que serve?

Podemos utilizar a equação da elipse para resolver problemas de geometria, e para desenhar gráficos. Vamos fazer um exercício para deixar tudo bem claro!

Descubra a equação da seguinte elipse:

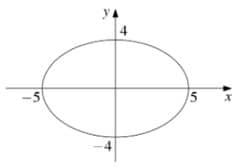
Com essa figura da elipse sobre os eixos cartesianos, podemos retirar algumas informações para descobrir a equação da elipse.

Primeiro podemos perceber que essa é uma elipse que tem o eixo maior sobre o eixo $x$, logo vai possuir uma equação com a cara:

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$

Então precisamos agora descobrir o valor de $a$ e $b$. Para descobrir o valor de $a$ que é metade do eixo maior, podemos visualizar na figura que o eixo maior tem um comprimento de 10 unidades de medida, por que vai de $x_1=-5$ até $x_2=5$. Logo nosso $a$ vale $\frac{10}{2}$, então $a=5$

Usando o mesmo raciocínio para o eixo menor encontramos que $b=\frac{8}{2},$ logo $b=4.$

E nossa equação da elipse fica:

$$\frac{x^2}{5^2}+\frac{y^2}{4^2}=1$$

Que pode ser reescrita como:

$$\frac{x^2}{25}+\frac{y^2}{16}=1$$