Equação da Parábola

A equação da parábola necessita de uma reta diretriz $d$ e um ponto que representa o foco da parábola $F$. O vértice da parábola deve estar no meio entre o $F$ e $d$, conforme a figura:

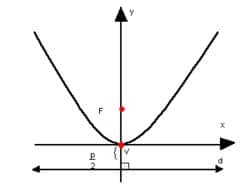
Se $p$ é a distância entre o foco e a reta diretriz, então a equação da parábola pode ser escrita como:

$$x^2=2py$$

É importante perceber que é possível rotacionar a parábola utilizando sinais negativos, ou alterando as variáveis, onde tem $x$ colocar $y$ e vice-versa, observe:

$$x^2=-2py$$

$$y^2=2px$$

$$y^2=-2px$$

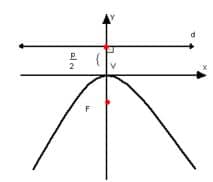
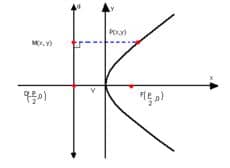
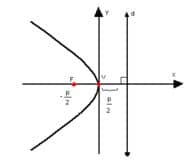
Para que serve?

A equação da parábola é o primeiro passo no estudo de equações do segundo grau, já que como sabemos equações do segundo grau, também representam parábolas, mas parábolas mais complexas e deslocadas em relação aos eixos cartesianos. A maioria das parábolas vão apresentar restas diretrizes paralelas ao eixo $x$ e $y$ e nesse caso podemos reescrever a equação da parábola naquele formato que já conhecemos:

Se a reta diretriz for paralela ao eixo x, a equação da parábola vira $y=a{x}^2+bx+c$.

Se a reta diretriz for paralela ao eixo y, a equação da parábola vira $x=a{y}^2+by+c$ .

Vamos resolver um exercício para deixar tudo bem claro!

Encontre a equação da parábola que passa pelos pontos $\left(0,0\right),(1,-1)$ e $(3/2,-1/2)$.

Para resolver esse exercício, vamos primeiro tentar descobrir qual a orientação dessa parábola, fazendo um esboço bem rápido, temos:

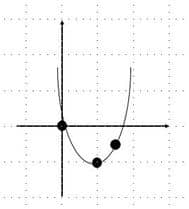
Então temos uma reta diretriz paralela ao eixo $x$ e nossa equação da parábola vai ter a carinha:

$$y=a{x}^2+bx+c$$

Para resolver o problema temos que achar os coeficientes $a,b$e $c$ e assim encontrar a equação da parábola, para isso vamos usar as informações sobre os pontos que a parábola passa e montar um sistema:

Ponto $(0,0)$:

$$0=a\times 0^2+b\times 0+c\to 0=c$$

Ponto $\left(1,-1\right):$

$$-1=a\times 1^2+b\times 1+c\to -1=a+b+c$$

Ponto $(3/2,-1/2$):

$$-\frac{1}{2}=a\times {\left(\frac{3}{2}\right)}^2+b\times \left(\frac{3}{2}\right)+c\to -\frac{1}{2}=\frac{9}{4}a+\frac{3}{2}b+c$$

Montando o sistema:

$$\left\{\begin{array}{c}c=0\\ a+b=-1\\ \frac{9}{4}a+\frac{3}{2}b=-\frac{1}{2}\end{array}\right.$$

Isolando $a$ na segunda equação:

$$a=-1-b$$

Substituindo na terceira equação:

$$\frac{9}{4}\left(-1-b\right)+\frac{3}{2}b=-\frac{1}{2}$$

Resolvendo a expressão, encontramos:

$$b=-\frac{7}{3}$$

Logo, resolvendo para $a:$

$$a=-1-b=-1-\left(-\frac{7}{3}\right)$$

$$a=\frac{4}{3}$$

Temos $a=\frac{4}{3}$, $b=-\frac{7}{3}$ e $c=0$, e nossa equação da parábola é:

$$y=\frac{4}{3}{x}^2-\frac{7}{3}x$$