Equação da parábola

Fala aí, você chegou no Responde Aí! E agora vamos entender um pouco sobre a Equação da Parábola.

A equação da parábola pode existir de duas formas:

• Equação reduzida da parábola: que relaciona a parábola a um foco e a uma reta diretriz
• Equação de segundo grau: que gera parábolas mais complexas

Equação Reduzida da Parábola

Você já tá ligado que uma parábola é um gráfico mais ou menos assim:

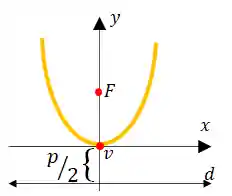
A equação reduzida da parábola necessita de uma reta diretriz e um ponto que representa o foco da parábola . O vértice da parábola deve estar no meio entre o e , conforme a figura:

Se é a distância entre o foco e a reta diretriz, então a equação reduzida da parábola pode ser escrita como:

Rotacionando uma parábola

Uma vez que a gente já tem a equação da parábola é possível rotacioná-la.

Adicionando um sinal negativo, a gente rotaciona a parábola em 180º. E se a gente trocar as posições do e do a parábola é rotacionada 90º

Observe:

Equação da parábola e Equação do 2º Grau

A gente já sabe que equações do segundo grau também geram parábolas, porém as equações do segundo grau geram parábolas mais complexas e deslocadas em relação aos eixos cartesianos.

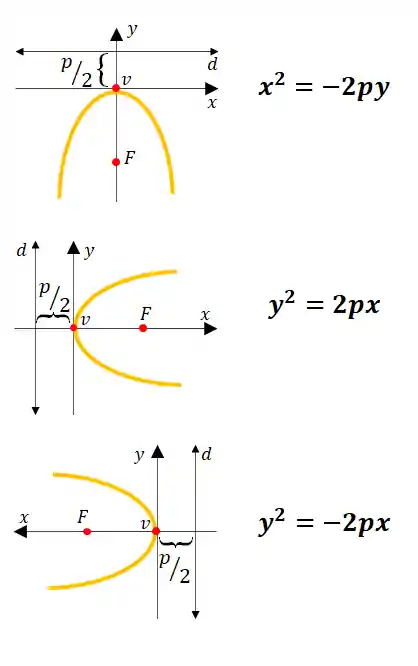
A maioria das parábolas vão apresentar restas diretrizes paralelas ao eixo x e y e nesse caso podemos reescrever a equação da parábola naquele formato que já conhecemos:

• Se a reta diretriz for paralela ao eixo , a equação da parábola vira .
• Se a reta diretriz for paralela ao eixo , a equação da parábola vira .

Exercício

Encontre a equação da parábola que passa pelos pontos , e .

Passo 1: Para resolver esse exercício, vamos primeiro tentar descobrir qual a orientação dessa parábola, fazendo um esboço bem rápido, temos

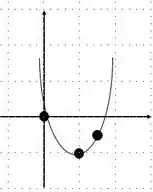
Então temos uma reta diretriz paralela ao eixo e nossa equação da parábola vai ter a carinha:

Passo 2: Para resolver o problema temos que achar os coeficientes a, b e c e assim encontrar a equação da parábola, para isso vamos usar as informações sobre os pontos que a parábola passa e montar um sistema:

• Ponto

• Ponto

• Ponto

Passo 3: Agora montamos o sistema:

Passo 4: Para resolver o sistema vamos isolar o na segunda equação

Passo 5: E aplicamos na terceira equação

Passo 6: E agora encontramos o valor de

Passo 7: E agora que temos o valor de , e podemos montar a equação da parábola: