Teoria
Introdução
Fala, galera! Esse é um assunto que muita gente já viu no ensino médio. Se você nunca estudou isso ou não se lembra de mais nada fique tranquilo. Vamos ver aqui tudo que você precisa saber pra ir bem na sua prova. Vamos dar uma relembrada rápida aqui.
Circunferência:
Vamos relembrar sua equação:
Essa é a equação da circunferência com centro em e raio igual a .
De maneira geral, a equação da circunferência de centro em e raio é:
Vamos ver dois exemplos:
Exemplo 1:
Encontre o centro e o raio da circunferência a seguir:
Comparando com a equação geral da circunferência :
Percebemos que , e
Exemplo 2:
Encontre o centro e o raio da circunferência a seguir:
Opa!!! Esse é diferente. Não ta nem parecido com a equação geral da circunferência. Então vamos colocá-la na forma:
Para isso, vamos completar os quadrados. Vamos começar ajustando os termos dependentes de .
Temos:
Ele nos faz lembrar . Mas não tem esse . Podemos fazer o seguinte:
Sacou? Eu somei e subtraí para que aparecesse o quadrado perfeito.
Observação: Perceba que , no caso acima:
Vamos fazer o mesmo raciocínio para os termos dependentes de :
Ajeitando temos:
Voltando a equação da circunferência:
Substituindo:
Então temos:
Portanto, a circunferência tem centro em e raio
Elipse:
Vamos relembrar sua equação:
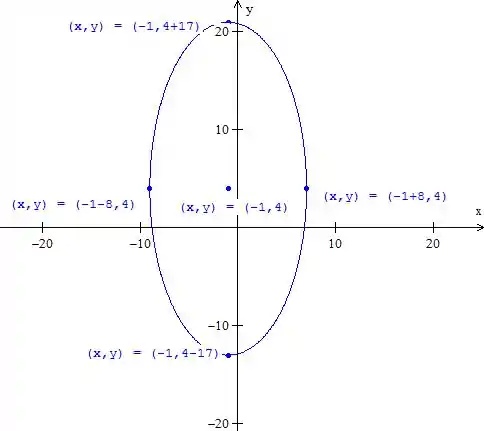
Essa é a equação da elipse com centro em , onde é o semieixo (metade do eixo) da elipse que se encontra ao longo do eixo e é o semieixo da elipse ao longo do eixo .
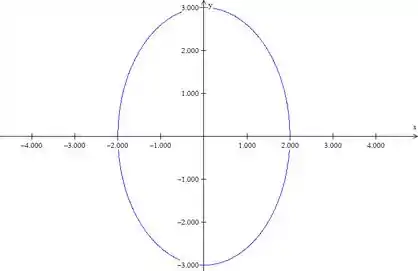
Na elipse mostrada na figura acima, percebemos que e 3.
De maneira geral, a equação da elipse com centro em e com semieixos e é:
Observação:
Perceba que se teremos:
Que é igual:
Que é exatamente a equação da circunferência.
Hipérbole:
Vamos relembrar sua equação:
Essa é a equação da hipérbole com centro em . E com vértices em e . Perceba que o eixo que contém a variável com sinal positivo, no caso eixo , corta a hipérbole em seus vértices.
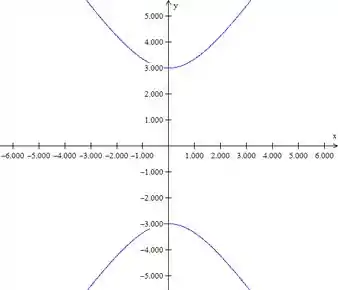
Uma outra possibilidade para a equação da hipérbole com centro em é a equação:
Sua “cara” é:

Essa hipérbole tem centro em e vértices em e .
Generalizando, a equação geral da hipérbole com centro em e vértices em e é:
Ou ainda:
Com centro em e com vértices em e
Parábola:
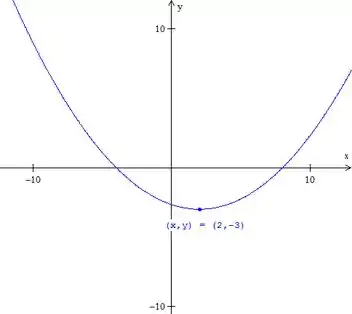
Vamos relembrar sua equação:
Essa é a equação da parábola com vértice e foco
De maneira geral, a equação da parábola com e foco é:
E tem essa cara:
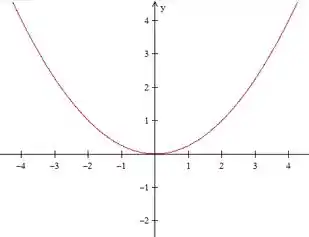
Pronto! Acabou a teoria! Bora praticar!!!
Elipse:
Hipérbole:
Parábola:
Exercícios Resolvidos
Exercício Resolvido #1
Gelson Iezzi, Fundamentos da Matemática Elementar, 7: geometria analítica, 5ªed. São Paulo: Atual, 2002, pp – 189 – 393 a,b,c – modificado
Caracterize a cônica representada por cada uma das equações abaixo e faça seu gráfico:
a)
b)
c)
Passo 1
- Bom, primeiramente vamos observar quantos termos elevados ao quadrado aparecem na equação e quais os seus respectivos sinais. A equação é:
- Bom, primeiramente vamos observar quantos termos elevados ao quadrado aparecem na equação e quais os seus respectivos sinais. A equação é:
- Bom, primeiramente vamos observar quantos termos elevados ao quadrado aparecem na equação e quais os seus respectivos sinais. A equação é:
Perceba que tanto quanto estão elevados ao quadrado e os seus sinais são iguais (ambos positivos).
Passo 2
Das cônicas que vimos na teoria, apenas a circunferência e a elipse tinham as duas variáveis elevadas ao quadrado e com o mesmo sinal. Provavelmente, a cônica dada nessa questão será uma delas.
Para provar isso, vamos ajustar a equação dada completando os quadrados. Vamos começar ajustando os termos dependentes de . Temos:
Podemos colocar o em evidência:
Vamos agora completar os quadrados da parte de dentro dos parênteses.
Perceba que nos faz lembrar . A única diferença é que esse “+4” aí não aparece. Podemos ajustar. Temos:
Eu apenas somei 4 e subtraí 4 dentro dos parênteses. Agora, temos o seguinte:
Ou seja:
Passo 3
Desenvolvendo o mesmo raciocínio para os termos dependentes de temos:
Colocando em evidência:
O termo nos faz lembrar . Podemos fazer o seguinte:
Ou seja:
Passo 4
Substituindo na equação da cônica dada temos:
Ajeitando a equação:
Chegamos então à:
Que é a equação de uma elipse com centro em e semieixos e .
Passo 5
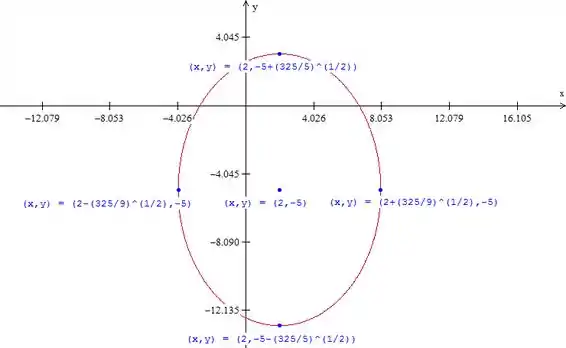
Vamos fazer seu gráfico. Marcamos o centro e os semieixos e desenhamos a elipse. Fica:
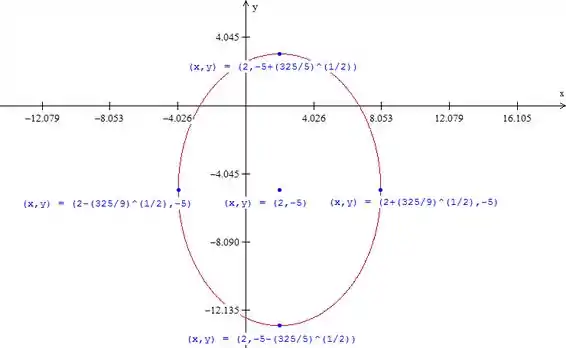
Passo 6
Perceba que tem grau 1 porém aparece com grau 2. Desconfiamos fortemente de uma parábola.
Passo 7
Arrumando a equação temos:
Vamos colocá-la na forma geral da parábola:
Ajeitando os quadrados fica:
Que é exatamente a equação da parábola com vértice em e foco
Passo 8
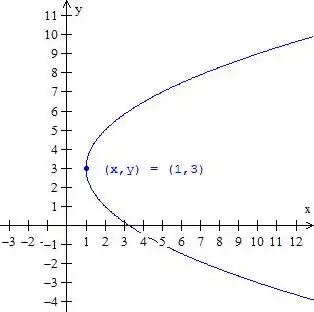
Para fazer seu esboço primeiro perceba que a variável elevada ao quadrado é . Marque o vértice. Fica:
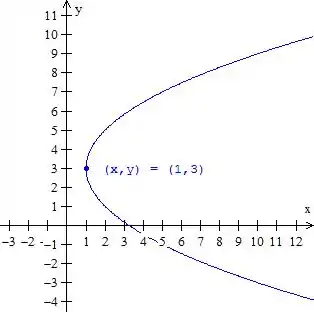
Passo 9
Perceba que tanto quanto estão elevados ao quadrado porém seus sinais são opostos. Desconfiamos de uma hipérbole.
Passo 2
Vamos tentar colocar essa equação na forma:
Ou
Vamos ajeitar os quadrados referentes a variável :
Passo 3
Fazendo o mesmo para a variável temos:
Passo 4
Substituindo na equação:
Tem de aparecer do lado direito, então vamos dividir tudo por :
Portanto a equação é uma hipérbole com centro em e vértices em e .
Passo 5
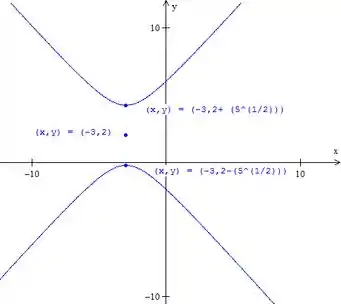
Para fazer seu gráfico, marcamos o centro e os vértices. Fica:
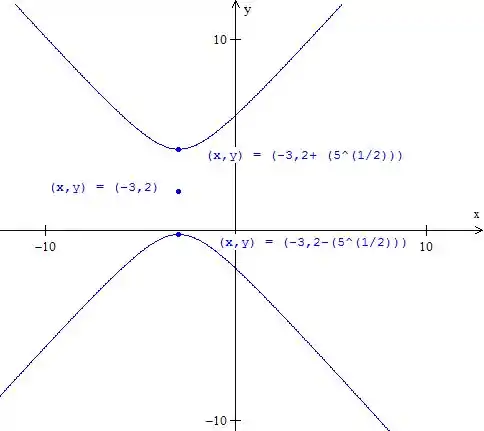
Resposta
- Elipse com centro em e semieixos e .
- Parábola com vértice em e foco
- Hipérbole com centro em e vértices em e
Exercício Resolvido #2
Gelson Iezzi, Fundamentos da Matemática Elementar, 7: geometria analítica, 5ªed. São Paulo: Atual, 2002, pp – 189 – 393 d,e – modificado
Caracterize a cônica representada por cada uma das equações abaixo e faça seu gráfico:
a)
b)
Passo 1
- Bom, primeiramente vamos observar quantos termos elevados ao quadrado aparecem na equação e quais os seus respectivos sinais. A equação é:
- Vamos observar quantos termos elevados ao quadrado aparecem na equação e quais os seus respectivos sinais. A equação é:
Perceba que apenas a variável está elevada ao quadrado. Desconfiamos de um parábola.
Passo 2
Arrumando a equação temos:
Vamos coloca-la na forma geral da parábola:
Ajeitando os quadrados fica:
Que é exatamente a equação da parábola com vértice em e foco
Passo 3
Para fazer seu esboço primeiro perceba que a variável elevada ao quadrado é . Marque o vértice. Fica:
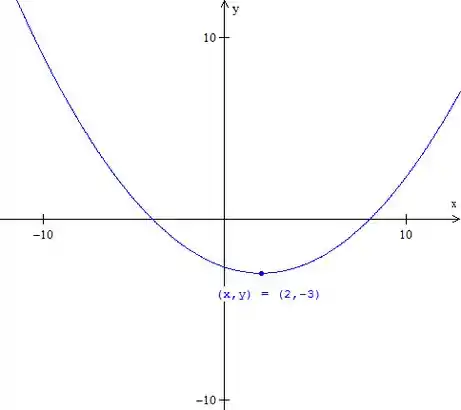
Passo 4
Que é o mesmo que:
Temos dois termos elevados ao quadrado de mesmo sinal. Desconfiamos de uma elipse ou circunferência.
Passo 2
Vamos coloca-la na forma:
Completando os quadrados temos:
Completando os quadrados de temos:
Passo 3
Substituindo na equação temos:
Ajeitando:
Que é a equação da elipse com centro em e semieixos e
Passo 4
Para fazer o gráfico, marcamos o centro e os semieixos:
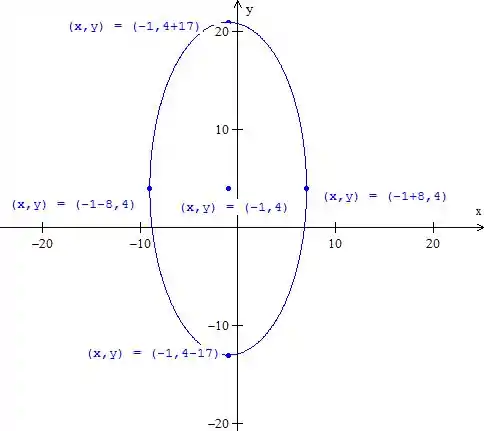
Resposta
- Parábola com vértice em e foco
- Elipse com centro em e semieixos e