Método dos Coeficientes Indeterminados
Teoria
Faaaala tu, tatu! Tudo bem? Hoje vamos estudar EDO de 2ª ordem não homogênea. Você lembra da homogênea? Ela era assim:
O problema todo surgiu quando essa mesma equação não estava mais igualada a zero! E agora? É isso que a gente vai estudar nessa teoria! Uma EDO desse tipo:
Onde e são constantes. A única diferença entre uma EDO homogênea e uma EDO não homogênea é esta: em vez de o lado direito ser igual a zero (homogênea), é igual a uma função de .
MAS CALMA AÍ, MEU ANJO! Não é qualquer função que vamos estudar aqui não. Serão EDOs desse tipo:
A função , em geral, envolverá no máximo três tipos de funções:
- Função exponencial:
- Função polinomial:
- Função trigonométrica: ou
Para resolver essas EDOs, são três etapas:
- Resolver a EDO como se fosse homogênea – solução homogênea:
- Encontrar a solução particular:
- Encontrar solução geral:
A etapa 1 já sabemos fazer, basta fingir que o lado direito da equação é zero, fazendo de conta que é uma EDO homogênea e então encontramos a solução homogênea
A etapa 2 será o foco dessa seção. Vamos ver passo a passo como encontrar o . Nada melhor do que começarmos com um exemplo, né?
Opaaaa! Primeira coisa a se fazer: encontrar . Para isto, é só resolvermos
Agora, bora pra particular! Cara, chegou a melhor parte disso tudo, hora de fazer algo que sabemos desde a escola: chutar!
Se a gente tem um , que é um polinômio, não há nada mais justo do que chutar um polinômio do segundo grau, não acha?
“Ahhh, mas só tem ali, pra que colocar o e o também?” Calma, você precisa chutar o polinômio por completo, não apenas a parte que aparece, ok?
Beleza, agora vamos substituir tudo na EDO.
Agrupando os termos semelhantes
Agora a gente só precisa comparar os coeficientes de ambos os lados.
Por exemplo, o cara que acompanha de um lado, tem que ser igual ao cara que acompanha o do outro lado. O cara que acompanha o de um lado tem que ser igual ao cara que acompanha o do outro. Esse raciocínio vai ser seguido sempre, ok?
Daí, resolvendo esse sistema, encontramos os valores de e , e substituímos em
E, finalmente, chegamos na etapa 3, encontrando a solução geral
Acabamos esse exemplo. Nem doeu, né?
Um passo MUITO IMPORTANTE é o seguinte: sempre que supomos um , precisamos ver se a nossa sugestão já está presente em . No exemplo acima não deu nada errado, porque não estava em , mas nem tudo são flores.
Olha um exemplo:
Esse é o mesmo caso que vimos agora, com exceção do , que é uma exponencial. Já vimos que a solução homogênea é
Já que temos uma exponencial, vamos chutar uma exponencial também, com o mesmo expoente, acompanhada por uma constante:
Show. Agora, perceba que esse chute já aparece em , concorda? Então precisamos consertar esse pequeno detalhe. Como fazemos isso? Vamos apenas multiplicar nossa por x até que ela fique diferente do termo que aparece em , desse jeito:
Prontinho, agora as contas seguem:
Agrupando os termos semelhantes
Logo, comparando os coeficientes em ambos os lados
Então,
Show?! Beleza, vamos ao último exemplo, envolvendo nossas trigonométricas (senos ou cossenos)
Novamente, . Como nossa ...
“Ahhhh, já sei, vou chutar , né?” NÃÃÃÃÃO!!! SEMPRE que aparecer senos ou cossenos, você precisa chutar uma combinação linear dos dois! O que é isso? É o seguinte:
Sacou? Agora o procedimento é o mesmo. Vamos verificar se ela está na solução homogênea... Não está, pois a homogênea desse caso só envolve exponencial. Podemos prosseguir:
Substituindo na EDO
Agrupando termos semelhantes
Novamente, vamos comparar os coeficientes:
Obtendo e
Então
Feitooooo!
Chegou a hora do BIZU! Dá uma olha na tabela aqui pra você saber qual chute dar!
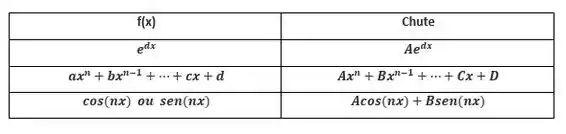
Nossa, falei muito! Guarda esse passo a passo e treina nos exercícios!
Passo a Passo
1. Resolva a equação homogênea (faça o ).
2. Identifique quem é o e compara com a tabela para determinar o seu chute.
3. Compare a solução homogênea e a particular. Se precisar vai multiplicando por até que elas fiquem diferentes.
4. Jogue o chute na EDO e descubra .
5. Se for um PVI/PVC, substitua os dados iniciais.
Passo a Passo
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Encontre a solução geral da equação diferencial abaixo:
Passo 1
Vamos seguir o passo a passo. Nosso objetivo é encontrar:
Primeiro, encontremos a solução da equação auxiliar, relativa a equação homogênea:
A solução homogênea é:
Passo 2
Partamos agora para a solução particular , ok? Se você observar, a parte não homogênea da equação (lado direito). O que temos lá? Uma trigonométrica, então pela tabelinha nosso chute vai ser:
Encontrando a primeira e a segunda derivada dessa solução particular, temos:
Passo 3
Agora temos que comparar a particular com a homogênea. Bem a homogênea envolve exponenciais e a particular trigonométricas. Portanto, não tem nada da particular na homogênea e podemos ficar com o seguinte palpite:
Passo 4
Agora temos que colocar essas derivadas na equação. Teremos, então:
Igualando o coeficiente que está multiplicando a função cosseno do lado esquerdo e do lado direito temos:
Como não há a função seno do lado direito da equação:
Então temos:
Passo 5
Assim, a solução geral é:
Porém encontramos:
Então fica:
Resposta
Exercício Resolvido #2
EDO de 2ª Ordem não Homogênea
Determine a solução geral da equação diferencial:
Com as seguintes condições iniciais
e .
Passo 1
a) Aqui temos uma EDO de segunda ordem não homogênea para ser resolvida. Basta a gente seguir o passo a passo que não tem o que dar errado! Nossa solução deve ser a forma:
Primeiro, encontremos a solução da equação auxiliar, relativa a equação homogênea:
Beleza, encontramos esses valores para ! Assim, como o foi maior do que , a solução homogênea é:
Passo 2
Partamos agora para a solução particular , ok? Se você observar, a parte não homogênea da equação (lado direito), é uma exponencial com . Pela nossa tabelinha devemos fazer
Passo 3
Agora temos que comparar e . Veja que está na solução homogênea. Ele é exatamente esse termo: . Então o que fazemos? Multiplicamos a particular por até que ela fique diferente
Beleza, ficou diferente. Agora podemos seguir no passo a passo.
Vamos achar as derivadas
Passo 4
Agora temos que colocar essas derivadas na equação. Teremos, então:
Devemos ter
Assim, a solução geral é:
Passo 5
b) Agora é substituir as condições iniciais nas equações que temos! Colocando em , temos:
Passo 6
Agora, vejamos o . Para isso, precisamos derivar , o que nos dá:
Colocando , teremos:
Passo 7
Agora, juntamos as duas equações e resolvemos o sistema:
Subtraindo a de baixo da de cima, teremos:
Substituindo esse valor para na primeira equação, temos:
Colocando esses dois valores na equação de , teremos:
Resposta
Exercício Resolvido #3
EDO de 2ª Ordem não Homogênea
Se , a equação diferencial tem uma solução da forma
(a)
(b)
(c)
(d) nenhuma das outras alternativas
(e)
Passo 1
Temos uma EDO não homogênea com a função no lado direito. Ele quer uma solução dessa EDO, então precisamos achar a solução particular.
Mas a gente não pode sair dizendo “ah então a solução é da forma !”. Primeiro a gente tem que calcular a solução da equação homogênea e depois a solução particular, show?
A EDO homogênea é
Assim, a equação auxiliar vai ser
Assim, vamos ter duas raízes iguais
Excelente! Asolução homogênea é da forma
Passo 2
Beleza, agora voltando à EDO não homogênea:
No lado direito temos algo do tipo então, como eu disse no começo, o nosso reflexo é tentar uma solução particular do tipo
Mas, atenção, primeiro temos que testar se essa opção é solução da equação homogênea!
E na solução da homogênea temos um termo então esse “chute” não serve!
Então vamos multiplicá-lo por , o que dá:
Mas novamente não vai dar certo porque na tem um .
Então temos que multiplicar de novo por :
Agora tá tudo certo! Essa é a solução particular da equação!
Juntando com a solução homogênea, obtemos a solução geral:
Passo 3
A nossa solução precisa ter essa cara
O que pode mudar aqui é esse e o , mas em todas precisa te algo com
A única alternativa que tem isso é a letra e, mas ele é somado com uma função que não tem nada de semelhante com a solução que achamos
Então nenhuma das alternativas está certa! Ou melhor, a alternativa “nenhuma das outras alternativas” está certa haha.
Resposta
Alternativa (d)
Exercício Resolvido #4
EDO de 2ª Ordem não Homogênea
- Determine o conjunto dos valores de tais que a equação diferencial
Possui uma solução particular da forma
Passo 1
Vamos achar o valor de para essa solução particular, devemos, primeiro, encontrar derivadas de :
Passo 2
Substituir na equação e encontrar constantes:
A solução particular vai ser dessa forma enquanto existir o valor de , então devemos ter
O conjunto vai ser