Modelagem - MHA e MF
Produzido por Carolina SabaTeoria
Movimento Harmônico Amortecido (MHA):
Movimentos harmônicos, no geral, são movimentos com a repetição de certo padrão. O sistema massa mola é um ótimo exemplo disso!
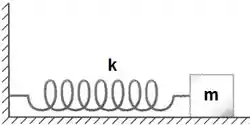
Beleza, mas disso você já desconfiava neh, agora eu quero ver você desconfiar dessa: o que são Movimentos Harmônicos Amortecidos?
ISSO MESMO! São movimentos harmônicos que de certa forma tem um “freio” amortecendo-o. Se pensarmos no sistema massa mola, tal “freio”, ou melhor, força de amortecimento, pode ser à força de resistência do ar que sempre tenta parar a massa!
Então o sistema não vai ficar oscilando pra sempre? Não! Ele vai parar com o tempo, porque a força resistente vai tirando energia do sistema até ele parar. Nesse caso, a energia não se conserva!
Dentre muitos MHA que existem na natureza, vamos falar do que cai na prova: Massa-Mola com amortecimento. Vamos ver o exemplo do sistema massa-mola imerso em um fluido viscoso:
A primeira coisa a se fazer é aplicar a Lei que descreve o movimento (Lei de Newton): pelo diagrama de Forças Livres...
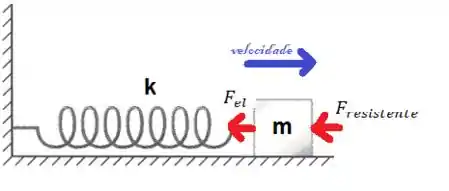
Observe que, nesse caso, além da mola com constante elástica , temos também uma força resistente, com constante de proporcionalidade . Pela Lei de Newton, a força resultante é a soma das forças:
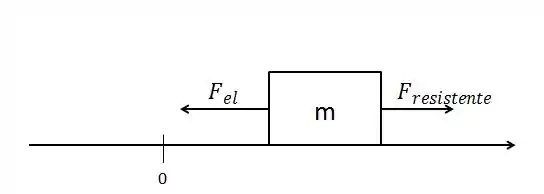
Imagine que o bloco está à direita do ponto de equilíbrio, se movimentando para a esquerda como na figura.
A força resistente do ar é dada por:
onde é a velocidade e é uma constante de proporcionalidade. O sinal de menos é porque a força resistente aponta sempre no sentido contrário ao movimento.
A força elástica é dada como sendo:
Onde é a constante elástica e o menos é pelo mesmo motivo do sinal de menos anterior.
Como de acordo com Newton sempre temos que a força resultante é dada pela massa vezes a aceleração...
Temos então:
Mas e
Opa, é uma EDO de segundo grau homogênea de coeficientes constantes, vamos dividir tudo pela massa:
Essa equação é a principal!
Assim podemos chamar
Vamos chamar:
Assim temos:
Já sabemos resolver uma EDO desse tipo. Vamos analisar os 3 casos:
- Caso 1:
- Caso2:
- Caso 3:
Para temos:
Então temos:
Quando dizemos que o sistema é criticamente amortecido.
Para temos:
Então temos:
Quando dizemos que o sistema é superamortecido.
Para temos:
Quando dizemos que o sistema é subamortecido.
Movimento Forçado (MF)
Até o momento só falamos de movimentos realizados por forças do sistema, seja o sistema sem forças resistivas, como o MHS, ou com essas forças como MHA. Mas o que acontece se a gente, fora do sistema, tiver forças que influenciam no movimento? Por exemplo:
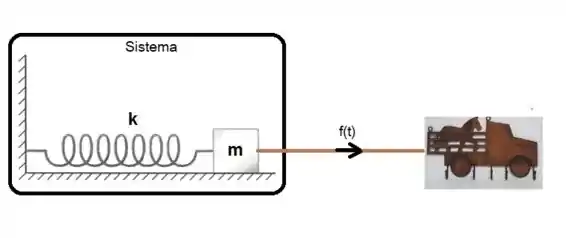
Nesse caso, devido ao fato de termos a força externa puxando a massa no sistema, podemos considera-lo como um Movimento Forçado. O movimento forçado ainda pode ser amortecido, quando a gente leva em consideração as forças de amortecimento, ou não amortecido.
Movimento forçado com amortecimento
Quando nós falamos em movimento forçado é quando possui uma força externa ao movimento. Assim, basta acrescentarmos essa força a equação. No caso do com amortecimento, temos:
Deixando somente do lado direito e dividindo pela massa:
Substituindo pelo que vimos acima:
Ficamos com:
Mas calma, o lado esquerdo continua o mesmo do movimento amortecido e o lado direito possui uma função em . Isso nós já vimos como resolver, essa é uma equação não homogênea. Assim, a solução é da forma:
A solução homogênea já vimos como resolver e a particular dependerá da cara de
Vamos agora ver o caso sem amortecimento, que é bem parecido.
Movimento forçado sem amortecimento
Esse caso é aquele que não possui o termo de amortecimento, no caso:
Assim, nossa equação se resumirá a:
Veja que essa equação também é não homogênea ela deve ser resolvida de forma que você encontre uma solução homogênea e a solução da equação particular.
Vamos agora resolver um exemplo para fixar melhor.
Exemplo:
Seja um sistema massa mola amortecido com:
Seja uma força de amortecimento:
E uma força externa atuante:
Com as condições iniciais:
Assim, encontre
Passo 1:
Primeiramente vamos montar a equação do movimento.
Ela é da forma:
Onde:
Então:
Passo 2:
Vamos agora encontrar solução homogênea:
Já aprendemos a resolver essa EDO.
Equação característica:
Raízes:
Solução da homogênea:
Passo 3:
Vamos agora encontrar com coeficientes a determinar:
Como é uma exponencial, também será uma exponencial de mesmo expoente:
Passo 4:
Encontrar derivadas de :
Passo 5:
Vamos substituir na equação e encontrar constantes:
Passo 6:
Assim, a solução geral é:
Passo 7:
Vamos agora aplicar as condições iniciais:
Calculando a derivada:
Calcular e :
Substituir condições iniciais dadas:
Resolvendo o sistema:
Substituindo na solução geral, encontramos a solução particular do PVI:
Partiu exercícios!!!
Movimento Forçado (MF)
Exercícios Resolvidos
Exercício Resolvido #1
UERJ - Cálculo 3 - Lista 6 Fernando Lopes – 4
Resolva o sistema de oscilações
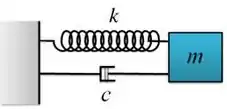
Passo 1
Vamos usar a segunda lei de Newton para conseguir montar a equação diferencial.
Mas para isso precisamos fazer o diagrama de forças atuantes. Fica assim:
Passo 2
Temos:
Então, pela segunda lei de Newton, a força resultante é dada pela soma de todas as forças atuantes:
Porém:
Temos:
Que equivale a:
Ajeitando:
Vamos usar o seguinte:
Então a EDO fica:
Passo 3
E como é que a gente resolve?
Quando temos uma EDO de 2ª ordem homogênea, resolvemos a equação auxiliar:
Assim:
Onde
Viu porque ele substituiu por Nego não ta de zoeira não! Cortou muita coisa
E então temos três possibilidades:
Em cada caso, temos uma solução diferente, lembra?
Então vamos analisar cada uma dessas possibilidades agora.
Mas antes vamos dar nome aos bois, mas relaxa com isso, é só para você entender o que tá acontecendo, esse tipo de nomenclatura não é cobrado na sua prova!
Quando : amortecimento subcrítico;
Quando : amortecimento crítico;
Quando : amortecimento supercrítico;
É só você lembrar que “sub” significa “abaixo” (abaixo de zero) e “super” significa “acima” (acima de zero).
Beleza?
Então vamos lá!
Passo 4
Nesse caso:
Então a equação auxiliar tem duas raízes reais e distintas:
E a solução é dada por:
As constantes e são dadas pelas condições iniciais de e .
O gráfico do amortecimento supercrítico tem essa cara(Só por curiosidade):

Uma soma de exponenciais decrescentes.
Passo 5
Nesse caso:
Então a equação auxiliar tem duas raízes reais e iguais:
E a solução é dada por:
Ou, se preferir colocar em evidência:
As constantes e também são dadas pelas condições iniciais de e .
E o gráfico do amortecimento crítico tem mais ou menos a mesma cara do amortecimento supercrítico(Isso é só por curiosidade!):

Passo 6
Nesse caso:
Então a equação auxiliar tem duas raízes imaginárias:
E a solução é dada por:
As constantes e são sempre dadas pelas condições iniciais de e .
E o gráfico do amortecimento subcrítico tem uma cara assim(Só por curiosidade again!!):
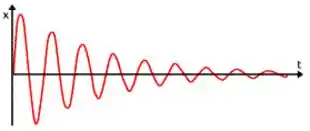
Nesse caso, o movimento é oscilatório, mas as amplitudes vão sendo cada vez menores, até parar.
Resposta
ou
ou
Depende da relação entre e !(Para saber se
Exercício Resolvido #2
UNA - Mecânica Aplicada - Vibrações Mecânicas
Para o pêndulo mostrado na Figura que modela um tipo de sismógrafo: determinar a frequência natural.
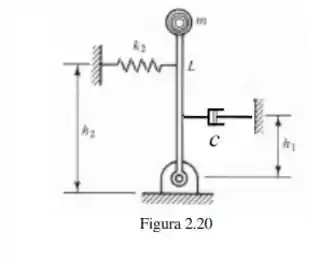
Passo 1
Primeiro vamos começar o problema, entendendo o que estamos buscando e como vamos chegar à solução. Ok?
Pois bem, estamos buscando a frequência natural do sistema harmônico com amortecimento . De acordo com a Teoria, se chegarmos a uma modelagem envolvendo uma EDO de 2º ordem como essa genérica aqui:
Então a frequência natural pode ser encontrada a partir do termo que multiplica . Então, no problema, basicamente devemos modelar o nosso problema e ver se a gente encontra algo parecido. Vamos nessa?
Passo 2
Para a modelagem, vamos começar partindo do modelo físico que rege o nosso sismógrafo: as Leis de Newton para pêndulos!
Em pêndulos, estamos interessados em saber qual é o ângulo a seguir com o tempo :
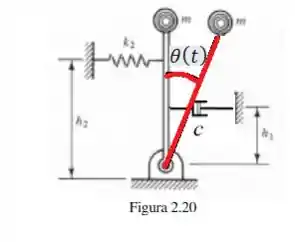
Basicamente, no problema temos três forças criando torques nesse pêndulo, o fazendo balançar com esse :
- Torque da força peso da bolinha .
- Torque da força elástica da molinha .
- E por último, Torque da força de amortecimento .
De acordo com Newton, a soma desses torques é um torque resultante e que é diferente , já que o pêndulo não está estático:
Vamos falar nos próximos passos, o que são cada torque representa. Vamos lá!
Passo 3
Primeiro vamos falar do torque resultante .
Toda vez que temos um pêndulo girando, então podemos calcular o torque resultante dessa forma aqui:
Onde é à distância da força ao ponto de rotação, enquanto é a força perpendicular ao movimento. Pelo diagrama a seguir, podemos ver quem é essa força:
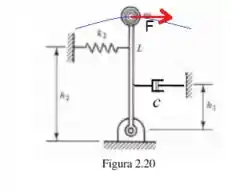
O movimento é sempre dado pela trajetória em azul. Como a trajetória em azul é um arco, então, podemos encontrar tal arco de acordo com a equação:
Ou seja, é o produto do raio pelo arco !
Sabemos que onde a aceleração é a derivada segunda da trajetória: :
Portanto, o Torque resultante será:
Passo 4
Vamos agora falar do torque causado pela força peso da bolinha:
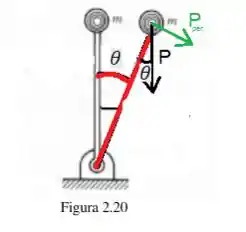
Veja que a única força que de fato importa não é nem o Peso em si, e sim a componente dela perpendicular ao movimento . Essa força pode ser obtida da seguinte forma:
Onde ...
Portanto, o torque causado por essa força peso será:
Como o ângulo é pequeno, podemos eliminar esse seno com uma ótima simplificação:
Logo, podemos dizer que...
Passo 5
Não desista, pois estamos indo bem, faltam ainda dois torques para analisarmos e vamos começar aqui com o :
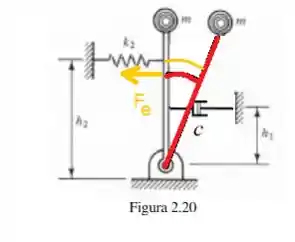
O torque dessa força elástica é dado por:
Onde é a distância de aplicação da força ao ponto de rotação. Enquanto que a força elástica é dada por:
Onde é a trajetória em laranja. De forma análoga ao cálculo da trajetória em azul no passo 3...
Ou seja, é o produto do raio, que agora é pelo arco...
Logo...
Passo 6
Beleza, agora vamos para o último torque que é o da força de amortecimento ...
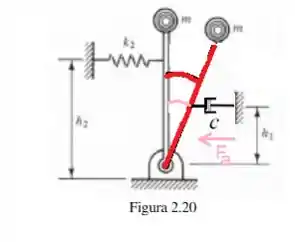
Agora, por definição de torque...
Onde é a força de amortecimento proporcional a velocidade...
A velocidade , entretanto, é a derivada primeira da trajetória circular em rosa dada por (assim como calculamos qualquer trajetória circular anteriormente é o produto do raio pelo arco )...
Logo...
Passo 7
Finalmente, depois de todos os torques calculados, podemos retornar para a igualdade do nosso querido passo onde deixamos o problema...
Substituindo todos os passos anteriores...
Passando tudo para um lado só...
Reorganizando...
Para comparar com essa EDO aqui
E descobrirmos quem é o , podemos dividir todos os termos por ...
Prontinho! De fato a equação que modela o nosso problema é uma EDO de 2º ordem, e podemos concluir que a frequência angular é...
Resposta
Exercício Resolvido #3
UNA - Mecânica Aplicada - Vibrações Mecânicas
Um voltímetro, mostrado na figura abaixo, possui um ponteiro de alumínio de comprimento , largura , e espessura . A mola restauradora tem uma constante de mola rotacional . Um amortecedor para amortecimento crítico é posicionado a um raio . Durante uma medida, o instrumento mostra . Quando a voltagem é desligada, determinar o tempo requerido para o ponteiro retornar à indicação de .
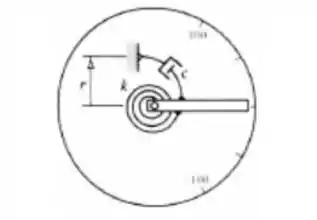
Passo 1
Antes de a gente começar, vou te dar algumas sugestões aqui, a final de contas, o nosso interesse é calcular uma EDO e não ficar procurando Momento de inércia de ponteiro (paralelepípedo), não é mesmo?
- Primeiro, vamos considerar o problema angular, onde o ângulo que o ponteiro faz com a horizontal depende do tempo : .
- Segundo, que se o problema é angular, então trabalhemos com torques!
- O Torque da força peso do ponteiro é , onde...
- E, caso precise, a velocidade do ponteiro, é de .
AHHH! Grande coisa! Mudou a minha vida saber disso!

Se você está agora como a Nazaré, então me siga !
Passo 2
Já vou te adiantando que esse exercício não é brincadeira, mas ao mesmo tempo é um problema de se apaixonar!
Para começar, vamos entender o que a gente busca no problema, ok?
Como o enunciado nos deu um valor inicial de medida (), trata-se de um problema de valor inicial, onde estamos buscando o tempo necessário para agulha retornar para a posição de desligado. Ora, a palavra chave desse problema, está em:
“Um amortecedor para amortecimento crítico é posicionado”
Essa é uma expressão fundamental, porque se você recordar na teoria, amortecimentos críticos, caso estivermos falando de uma EDO de ordem, possuem uma equação dessa forma aqui:
Ora! Nós temos o tempo inicial quando medimos , falta encontrarmos o tempo final . Daí, o tempo para o ponteiro retornar à indicação de será , o valor buscado no problema!
AHA! Então isso significa que estamos no caminho certo! Mas infelizmente, essa expressão só funciona, caso estivermos falando de uma modelagem envolvendo equações diferenciais de ordem. Então para responder o problema, precisamos averiguar as respostas para essas perguntinhas aqui:
- A modelagem é uma equação de ordem? Se for, quem ela é?
- Quem é e ?
- Quem é ?
Após essas perguntas, é fácil encontrar , bastando substituir!
Passo 3
Primeiro vamos responder a primeira e uma das mais importantes perguntas da rodada: A modelagem é uma equação de ordem? Se for, quem ela é? É com essa pergunta, que vãos (vamos) de fato averiguar se a equação do amortecimento acima pode ser usada.
O problema que estamos lidando, é um problema regido pela mecânica Newtoniana. Então vamos começar listando os torques envolvidos no problema:
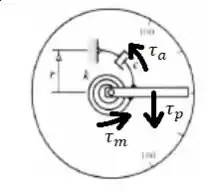
- Temos o torque causado pela força peso do ponteiro .
- Temos o Torque causado pela mola .
- E temos o Torque causado pela força de amortecimento .
De acordo com a Lei de Newton, o torque resultante é a soma dos outros dois, para o sistema entrar em equilíbrio:
, de acordo com a sugestão, é dado por:
Onde:
é o momento de inércia do ponteiro:
é a aceleração angular:
, por sua vez, é dado por:
(OBS de física: esse é a constante de mola rotacional, portanto vezes o deslocamento angular já é o torque, diferentemente de , onde esse não é rotacional, então o produto nos dá a força).
Enquanto isso, :
Onde:
é a constante de amortecimento;
é a velocidade do ponteiro, dado por .
Juntando tudo na expressão Newtoniana de torque resultante:
Simplificando um pouco...
Pelo enunciado, sabemos que:
Então...
Agora é só simplificação, veja:
Ou...
Veja que de fato a modelagem é uma EDO de segunda ordem!
Passo 4
Com isso, estamos prontos para responder a segunda pergunta: Quem é e ?
Sabemos que a resposta dessa equação, devido ao fato de estarmos trabalhando com um amortecimento crítico, será da forma:
Sabemos também, que a tensão no tempo inicial é . Mas agora, que ângulo isso corresponde?
Pela posição no desenho,
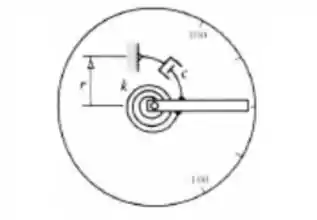
é . Agora não tem como de saber, neh? Na verdade, também não é tão relevante assim. Então se chamarmos de um ângulo de , onde um ângulo qualquer que a gente não conhece, então com uma regrinha de 3, o ângulo correspondente a ...
(No final das contas, o que está valendo é a proporção, está vendo?)
Sabemos também que por se tratar de uma equação de segunda ordem, temos que ter a velocidade no tempo inicial! Como no tempo inicial, o ponteiro estava parado, então...
Essas são as condições iniciais:
Passo 5
Descobrindo substituindo a primeira condição na equação...
Como ...
Logo...
Passo 6
Descobrindo usando a segunda condição . Logo a gente precisa derivar a equação...
Substituindo tudo o que conhecemos...
Logo...
Ou
Estamos prontos agora para descobrir quem é ...
Passo 7
A última pergunta (quem é ?) pode ser respondida lembrando que é a frequência de oscilação sem amortecimento, pode ser obtida através da equação de modelagem do sistema assim:
Então, a nossa equação de amortecimento crítico final é...
Passo 8
Só falta então, finalmente encontrarmos o tempo final comentado lá no passo para fecharmos o problema com chave de ouro:
Sabemos que no tempo final , temos a tensão de , em termos de ângulo, isso quer dizer . Logo,
Com um auxílio de uma calculadora a gente descobre que então esse é o tempo que a agulha demora a retornar ao ponto inicial!
Eu sei! Foi um problema grande e que necessitou da calculadora em vários momentos, mas vai falar que não é um problema elegante? :D
AH! E só mais uma coisa, esse é um problema de mecânica, por isso se isso cair na sua prova de cálculo, não se preocupe! O seu professor vai te dar aquelas sugestões como nós demos aqui, afinal, você não é obrigado a se lembrar de momento de inércia de um ponteiro (paralelepípedo) !