Campos Singulares
Teoria
Dá uma olhada nesse campo aqui
e a curva que delimita a região .
A curva que temos é uma circunferência de raio centrada na origem, o problema é que não podemos usar o teorema de Green por que ele tem uma restrição que quase ninguém lembra: o campo tem que ser definido em toda região de integração.
Campos Singulares
“Ah, a gente nunca parou pra ver isso, o que seria um campo que não está definido? ”
Bem, normalmente, o campo está sempre definido, por isso não ligávamos muito. Só temos pontos de indeterminação (ou singularidade) quando temos aqueles bugs da matemática, tipo divisão por , raiz quadrada de número negativo, essas coisas que costumam dar problema.
Voltando para o nosso campo ali de cima
Perceba que a origem é o ponto em que o campo possui uma singularidade! Pra usar o teorema de Green aqui, a gente vai ter que dar uma roubada, olha só o que podemos fazer
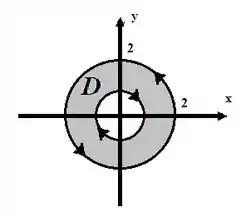
O círculo menor possui um raio igual a 1, para facilitar as contas. A nossa curva, nesse caso, pode ser separada em duas, sendo a de fora e a de dentro.
Lembre-se que a orientação dela é muito relevante. Precisamos da orientação positiva, se você não lembra disso, dá uma olhada no tipo de curvas compostas, beleza?
Com isso, teremos que e:
E agora sim, , a fronteira para uma região onde é válido aplicar o teorema.
Portanto, teremos:
Onde a integral de linha de é a que nos queremos, então:
E assim fazemos para quantos pontos de indeterminação forem necessários. O princípio básico é conseguir fugir de todos esses pontos (as vezes tem mais de um) e, assim, vamos isolando um por um com curvas.
Passo-a-passo
Passo 1: Montar o problema
Passo 2: Isolar a singularidade
Passo 3: Calcular a integral dupla
Passo 4: Calcular a integral de linha sobre a curva interna
Passo 5: Somar tudo
Eu sei que é muita coisa, mas calma, é só ter esse passo a passo na cabeça que as questões não fogem muito disso. Vamos lá ver os exercícios, então?
Campos Singulares
Passo-a-passo
Exercícios Resolvidos
Exercício Resolvido #1
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp.245-8.
Sejam e funções reais de classe e ( e como na figura), tais que em . Sendo , , as curvas dadas na figura, calcule , supondo que:
Passo 1
O exercício nos pede pra calcular o integral de linha vetorial escrita na forma:
Mas não temos muita informação sobre o campo , apenas sobre as derivadas de suas componentes, .
Por sorte isso, isso já é o suficiente pra calcularmos o teorema de Green:
Até ai tudo bem, né? O problema é que a nossa curva não satisfaz as condições do teorema, porque não é simples e o campo não é definido em toda a região limitada pela curva por causa dos pontos e .
Mas calma que tem solução pra isso, vamos ver como fica!
Passo 2
Primeiro, vamos dividir a curva em dois pedaços, para garantir que, assim, teremos duas curvs simples. Dessa forma, vamos chamar de e (podemos ver que esse pedaço está no sentido horário e, portanto, botamos esse sinalzinho para identificar a orientação negativa) os pedaços:
Agora sim temos duas curvas fechadas e simples, de forma que:
Agora só temos que resolver as singularidades.
Passo 3
Lembra que podemos criar curvas com “buracos” pra usarmos no teorema de Green?
Se fizermos então:
(Lembrando que as curvas internas devem ter orientação positiva, no sentido horário. E as curvas externas, orientação positiva, no sentido anti-horário.)
Com isso, temos que as regiões limitadas por e são válidas, então e , e podemos aplicar o teorema de Green:
E
Então vamos resolver uma por uma pra ver como que fica!
Passo 4
Na primeira, vamos ter:
Que é dado na questão, então:
Passo 5
Para a segunda, vamos ter:
Que também foi dado:
Passo 6
Por fim, vamos só jogar esses valores na integral que tinhamos lá em cima, vamos lembrar:
Resposta
Exercício Resolvido #2
Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, pp. 228
Calcule a integral de linha do campo vetorial
ao longo da curva de equação orientada no sentido anti-horário.
Passo 1
Vamos fazer um esboço da curva:
Essa integral de linha parece um pouco complicada de se calcular diretamente pela definição. Vamos, então, usar o Teorema de Green.
Mas aqui temos um problema: o campo não está definido em toda a região dentro da elipse, pois temos uma descontinuidade na origem, se substituirmos na função teremos zero no denominador. O que faremos então? É simples, basta tirarmos a origem da jogada. Se fizermos uma circunferência que “envolva” a origem e chamarmos de a região entre a circunferência e a elipse, o problema está resolvido. Faremos um circunferência de raio para facilitar nossos cálculos. Vamos fazer o novo gráfico para ver como fica essa parada
Temos então:
Passo 2
Vamos agora calcular :
Passo 3
Aplicando o teorema de Green, temos:
A área de é a área da elipse, dada por (onde e são seus semieixos) menos a do círculo. Então:
Guarde esse resultado. Agora vamos calcular a integral ao longo da circunferência.
Passo 4
Parametrizando a circunferência, temos: com variando de a (pois a circunferência está orientada no sentido horário, contrário ao trigonométrico).
Temos
Você poderia utilizar o intervalo de a desde que considerasse que essa integral teria sinal oposto, pois:
Passo 5
Substituindo esses valores na fórmula que vimos capítulo passado:
Temos:
Passo 6
Agora vamos calcular o valor dessa integral. Para isso usaremos a equação do arco duplo:
Passo 7
O que queremos calcular é a integral de linha ao longo de , certo? Substituindo os valores que encontramos em:
Temos:
Resposta
Exercício Resolvido #3
UFF - Cálculo IIIA - Lista 4, GMA 2015.2 – 24
Calcule
Onde é a curva , , orientada de à
Passo 1
Vamos fazer um esboço da curva:
Essa integral de linha parece um pouco complicada de se calcular diretamente pela definição. Vamos, então, usar o Teorema de Green.
Repara que a curva não é fechada, para aplicarmos o teorema de Green devemos fechar essa curva.
Mas aqui temos um problema: o campo não está definido em toda a região dentro da elipse, pois temos uma descontinuidade na origem, se substituirmos na função teremos zero no denominador. O que faremos então? É simples, basta tirarmos a origem da jogada. Como temos que completar essa curva vamos pegar essa curva completando sem a origem.
Vamos fazer onde é uma circunferência de raio e centro na origem. A equação de vai ser
Pegamos uma circunferência de raio porque o gráfico vai ficar assim
Veja que não é positivamente orientada, pois deixa a região a direita. Devemos usar então:
Passo 2
Vamos agora calcular :
Passo 3
Logo, temos que resolver o seguinte:
Temos que fazer a integral de linha e a integral dupla, vamos começar pela integral de linha.
Passo 4
Parametrizando a semicircunferência, temos:
Com variando de a
Substituindo esses valores na fórmula que vimos capítulo passado:
Temos:
Vamos separar essa integral em duas
Passo 5
Começando com
Lembrando que
Vamos ter,
Passo 6
Vamos para a outra integral agora
Vamos fazer a integral indetermina, ignorando por enquanto os limites e o
Vamos fazer
Então
E a integral vai ficar
Resolvendo a integral vamos ter
Voltando para
Vamos voltar para a integral com os limites e o
Passo 7
Então, nossa integral de linha resulta em:
Passo 8
Vamos agora para a integral dupla,
Onde é a parte de dentro da circunferência e de fora da elipse
Antes de tudo vemos que essa integral vai ser
Passo 9
Vamos voltar para o gráfico que vimos antes.
A área de vai ser a área da semicircunferência menos a da semielipse, ou seja
Passo 10
Vamos agora para a integral com
Como temos várias coisas circulares é jogo usarmos coordenadas polares né? Então
A equação da elipse é:
Então, nossos limites são:
E como estamos no primeiro e segundo quadrantes:
Substituindo na integral:
Integrando em :
Separando em duas integrais:
Os novos limites de integração são:
Opa, já deu pra ver o que vai rolar né? Uma integral indo de até vale !! Então:
Passo 11
E ficamos com:
Passo 12
Agora pra finalizar (FINALMENTE!!!!):
Resposta
Exercício Resolvido #4
UFRJ - Cálculo 3 - P1 2010.2 - 4
Seja uma curva parametrizada por , por partes como no esboço abaixo tal que e . Calcule
Passo 1
Como não temos a equação dessa curva para calcular a integral de linha pela definição, vamos aplicar o Teorema de Green.
Como a curva não é fechada, precisamos criar uma curva que ligue os pontos e , que chamaremos de . Perceba que o campo vetorial não está definido na origem , pois teríamos zero no denominador, assim, não pode ser uma reta. Mais à frente veremos que curva será essa. Orientando positivamente as duas curvas, teremos, então:
Passo 2
O campo vetorial pode ser escrito como
Vamos agora calcular :
Passo 3
Aplicando o teorema de Green, temos:
Passo 4
Agora precisamos resolver a integral ao longo de , mas que curva será essa? Já que não podemos escolher uma reta, vamos ver que expressão poderia simplificar nossas contas. Veja que nas duas componentes do campo vetorial, temos o termo no denominador, que se assemelha à expressão de uma elipse.
Se escolhermos a parte com da elipse para ser essa curva, teremos para sua parametrização, certo? Com variando de até para a orientação ser positiva. Veja que a origem está fora da região limitada pelas curvas.
Assim, teremos nos denominadores, o que simplifica bastante.
Passo 5
Agora vamos calcular :
Passo 6
Substituindo esses valores na fórmula
Temos:
Passo 7
Agora vamos resolver essa integral:
Passo 8
Como temos
A integral que buscamos será
Resposta
Exercício Resolvido #5
UFRJ - Cálculo 3 - PF 2014.1 – 2
Calcule a integral de linha do campo
Ao longo de uma curva fechada simples orientada positivamente e satisfazendo as duas seguintes propriedades:
- O círculo de centro em e raio está no interior da região limitada pela curva ;
- A área da região delimitada por é .
Passo 1
Bom, se a questão relaciona uma integral de linha com uma área (integral dupla), já sabemos que estamos falando de Green. Ainda mais porque ela não nos dá essa curva .
Certo, se estamos falando de Green, vamos começar calculando o termo :
Passo 2
Agora vamos aplicar Green, mas com calma. Repare que temos uma singularidade no ponto (o denominador do campo dá zero), portanto, precisamos excluir ese ponto da região.
Bom como a questão fala que O círculo de centro em e raio está no interior da região limitada pela curva , vamos usar esse círculo para isolar o ponto (repare que o ponto está dentro dele). Bom, isso pode não ser uma boa ideia por causa do denominador do campo: .
Seria muito melhor se a gente isolasse esse ponto com a circunferência .
E nós podemos fazer isso, porque essa circunferência está dentro da cicunferência de raio centrada na origem, que o problema afirma estar dentro de . Portanto, a circunferência de raio deslocada também está dentro de !
Então, vamos isolar o ponto com essa nova circunferência.
Sendo, então, a região entre e essa circunferência deslocada e sendo orientada no sentido anti-horário e a circunferência horário, temos:
A questão também fala que a área da região delimitada por é . Podemos escrever então:
Como a circunferência tem raio , sua área é dada por :
Passo 3
Agora falta a integral na circunferência. Vamos parametrizá-la em coordenadas polares deslocadas com :
Como ela gira no sentido horário, vai de a . Agora derivamos isso aí:
Aplicamos a fórmula:
Lembrando que
Passo 4
Temos, então:
Resposta
Exercício Resolvido #6
USP - Cálculo 3 - P2 2015 - 3
Seja o campo e seja a curva que é fronteira da região limitada pelos gráficos das funções e percorrida no sentido horário. Calcule .
Passo 1
Vamos fazer um esboço dessa curva . Temos duas funções:
São duas parábolas com eixo de simetria paralelo ao . A segunda, na verdade, tem eixo de simetria no próprio eixo e tem concavidade para cima (por causa do sinal positivo no ). Já a primeira tem concavidade para baixo e é deslocada em relação ao eixo :
A curva é então isso aqui:
Como o enunciado fala, ela é percorrida no sentido horário.
Onde
Beleza? Então, podemos escrever:
Bom, já que temos uma curva fechada e um campo com expressão bizarra, vamos usar Green, né? Vamos fazer isso para cada parte do campo, separadamente.
Passo 2
Para o campo
Aqui nós temos um problema, se você reparar, o campo não está definido em , que pertence ao interior da nossa curva .
Vamos, então, fazer uma outra curva que envolva esse ponto (orientada no sentido horário) e considerar nossa região como o anel formado pelas duas curvas.
Beleza, conseguimos tirar o ponto da jogada tornando nossa região um anel, agora podemos aplicar Green.
Onde é o anel que está entre as duas curvas. Repare que, como é orientada no sentido horário (negativamente), tivemos que usar para aplicar o teorema. Já , é orientada positivamente (sentido horário). Isso é o mesmo que:
Temos então:
Ótimo, o campo é conservativo. Isso nos dá que:
Ok, agora vamos ver quem é .
Agora repara o seguinte, temo no denominador do campo... Parece uma elipse (deslocada), não é? Não seria muito bom se a nossa curva fosse uma elipse desse tipo? Olha só, vamos definir a elipse :
Repara que ela isola o ponto da nossa região, pois esse é o seu centro. Percebeu?
Sua parametrização, em coordenadas elípticas é:
Quando a gente aplicar isso aí na função do campo, as coisas vão ficar muito mais simples, porque o termo vai virar 1. Olha que lindo né.
Para nossa curva estar orientada positivamente, já vimos que a elipse deve ser percorrida no sentido horário, ou seja, vai desde até .
Vamos calcular agora a derivada dessa parametrização:
Então, usando a definição de integral de linha, podemos escrever o seguinte:
O campo
Escrito em termos da parametrização, fica
Substituindo o campo, a derivada da parametrização e os seus intervalos na integral, temos:
Calma que não acabou, ainda falta o campo !
Passo 3
Para o campo
Vamos lá, gente, força, quase acabando. O outro campo é o seguinte:
E nós queremos
Bom, como esse campo não tem nenhum problema com singularidade, podemos usar só a curva do enunciado para limitar nossa região, né? Vamos aplicar Green nesse aqui:
Temos então
Temos, de novo, a mesma questão da orientação aqui!
Onde é a região dentro de . Agora é só resolver essa integral dupla aí.
Vamos escrever a região como tipo I, está entre as equações das parábolas e entre e , como podemos ver na figura do passo 1. Para achar esses valores de , nós igualamos as equações das parábolas e descobrimos onde elas se encontram:
Levando para a integral, temos:
Passo 4
Como nós dissemos lá no início, a integral que queremos é dada por:
Substituindo os valores que encontramos