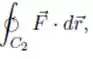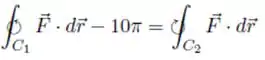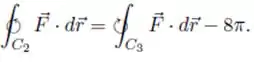Exercícios de Campos Singulares - Lista de Exercícios Resolvida

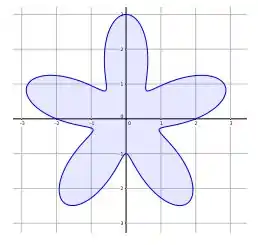
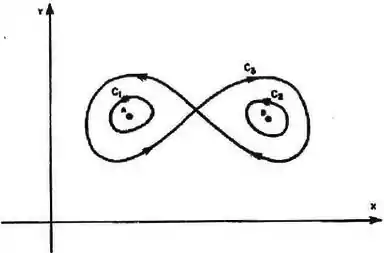
Sejam e funções reais de classe e ( e como na figura), tais que em . Sendo , , as curvas dadas na figura, calcule , supondo que:

Calcule a integral de linha do campo vetorial

ao longo da curva de equação orientada no sentido anti-horário.

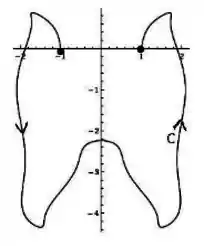
Seja uma curva parametrizada por , por partes como no esboço abaixo tal que e . Calcule

Calcule

Onde é a curva , , orientada de à

Calcule a integral de linha do campo

Ao longo de uma curva fechada simples orientada positivamente e satisfazendo as duas seguintes propriedades:

1. O círculo de centro em e raio está no interior da região limitada pela curva ;
2. A área da região delimitada por é .

Seja o campo e seja a curva que é fronteira da região limitada pelos gráficos das funções e percorrida no sentido horário. Calcule .

Considere o campo:

Determine onde é a fronteira do quadrado de vértices , , e orientada no sentido horário.

Calcule , onde

E é a circunferência unitária orientada no sentido anti-horário.

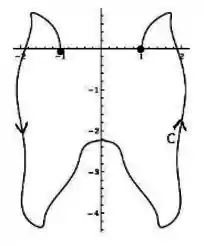
Seja uma curva parametrizada por , por partes como no esboço abaixo tal que e . Calcule

Seja a fronteira da região de limitada por e , percorrida uma única vez no sentido anti-horário. A integral é igual a:

Calcule , onde é a curva dada por , , orientada de a .

25) Seja

Calcule a integral de linha do campo ao longo de e , orientadas no sentido anti-horário, onde

21) Seja um campo vetorial de classe , em tal que , para todo . Sabendo que , onde , calcule

Onde .

Encontre todos os valores possíveis de

Onde é uma curva fechada qualquer que não passa pela origem.

Seja

Calcular a integral de linha vetorial , onde é a curva união das curvas planas e :

é a fronteira do quadrado orientada no sentido anti-horário

é a fronteira do quadrado orientado no sentido horário

Questão 4: Calcule onde é a fronteira do retângulo percorrida uma vez no sentido anti-horário e

Seja

E a curva percorrida uma vez no sentido anti-horário. Calcule .

3) Seja

um campo de classe em . Seja a curva dada pela concatenação do segmento que une a , o arco da circunferência com centro na origem, sentido anti-horário, indo de a e o segmento que une a .

Calcule

Sugestão: Construa uma curva que “feche” a curva adequadamente, de modo que seja possível usar o Teorema de Green na região que tem a curva fechada como fronteira.

Considere o campo vetorial dado por

1. Mostre que , onde é a circunferência .
2. O campo é conservativo em ? Justifique.
3. Sendo , mostre que .
4. Mostre que para toda curva fechada simples que circunde a origem.

Questão 4:

Calcule a integral

quando

1. é o círculo .
2. é a elipse .

Seja

Calcule onde é a curva , orientada no sentido anti-horário.

Seja um campo vetorial tal que , contínuo em , onde é uma constante positiva. Suponha que

Onde é dada por , orientada no sentido anti-horário. Calcule a integral de linha vetorial

Onde é dada por, orientada no sentido anti-horário.

23) Calcule onde

e é a curva fechada formada pelas curvas , e , , percorrida no sentido anti-horário.

Seja um campo vetorial definido em . Calcule a integral ao longo das curvas e , orientada no sentido anti-horário, onde:

1. é a circunferência da equação .
2. é a fronteira do retângulo .

Calcule

Sendo o arco da curva que liga a

Considere o campo

com ∈ . Usando Green, resolva as seguintes questões:

a) Desenhe a região limitada por , e e selecione uma parametrização orientada positivamente para seu contorno (ou orientada anti-horáriamente).

b) Determine os valores do parâmetro a de modo que a integral .

c) Calcule a integral de linha do campo para o valor .

Questão 4: Calcule a integral de linha do campo vetorial

Ao longo do círculo (circunferência) orientado no sentido anti-horário.

Seja o campo e seja a curva que é fronteira da região limitada pelos gráficos das funções e percorrida no sentido horário. Calcule .

24) Calcule

Onde é a curva , , orientada de à

3) Calcule , onde e

Use o teorema de Green para calcular a integral de linha

Em que é a curva mostrada abaixo, orientada no sentido anti-horário e dada por

Calcule a seguinte integral de linha de campo vetorial:

Ao longo da curva , união das curvas definidas por:

• , a curva percorrida no sentido horário,
• , a curva percorrida no sentido anti-horário.

22) Considere um campo definido em tal que em . Suponha que , e , . Calcule

28) Seja de classe em , tal que , sejam , e . Calcule

Sabendo que

e

Seja

um campo vetorial em . Calcule a integral de linha do campo ao longo da curva , orientada no sentido anti-horário, onde:

é a fronteira do retângulo .

Calcule a integral de linha do campo

Ao longo de uma curva fechada simples orientada positivamente e satisfazendo as duas seguintes propriedades:

1. O círculo de centro em e raio está no interior da região limitada pela curva ;
2. A área da região delimitada por é .

Sejam

e

Calcular a integral de campo vetorial , onde é a curva , para .