Teorema Fundamental do Cálculo com L’Hospital
Produzido por Arthur Melo de AlmeidaTeoria
Misturando limites e integrais
Existe uma aplicação do Teorema Fundamental do Cálculo que é calcular limites que caem em indeterminações. Isso mesmo: aqueles limites que dão ; , ... e que aí você tem que usar L’Hospital para resolver.
Pode parecer esquisito misturar L’Hospital com Teorema Fundamental do Cálculo. Mas lembra que, quando você cai em uma indeterminação do tipo ou , você aplica L’Hospital, né? E o que significa isso? Derivar em cima e embaixo, não é mesmo?
Então, às vezes o cara coloca uma expressão do tipo:
Ali no meio do limite. E aí ele faz de uma forma que você cai numa indeterminação, de forma que você vai ter que aplicar L’Hospital.
Para isso, você vai ter que saber derivar uma função desse tipo. Quem te ensina isso? O Teorema Fundamental do Cálculo – Parte 1 \o/
Vamos parar de blá blá blá e fazer um exemplo para você ver na prática como funciona?
Exemplo 1:
Quando vamos calcular um limite, a primeira coisa que fazemos é substituir o valor que ele dá na função que está dentro do limite para ver o que acontece. Nesse caso, se fizermos na expressão dada, olha o que acontece:
Já sabemos, pelas propriedades de integrais, que uma integral com limites de integrações iguais é nula. Portanto: TCHARAM! Temos uma indeterminação do tipo:
E aí? Qual a forma mais simples de resolver isso aí? Não é aplicando o famoso L’Hospital?
Para derivar o numerador temos que usar o Teorema Fundamental do Cálculo:
Lembra como deriva aquilo ali? O limite de integração superior é uma função de . Então primeiro substituímos a variável dentro da integral por essa função de e depois aplicamos a regra da cadeia:
Agora que acabamos com a indeterminação, podemos substituir:
Pronto! É só correr pro abraço e fazer umas questõezinhas para treinar, combinado?
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ - Cálculo 1 - P2 2008.2 -
Calcule o limite:
Passo 1
Bom, temos limite misturado com integral de uma função da forma:
Fica esperto que isso tem muita cara de que quando você substituir o limite, vai cair em uma indeterminação. Aí vai ter que aplicar L’Hospital e usar o Teorema Fundamental do Cálculo – Parte 1 para calcular a derivada dessa função que está no numerador. Quer apostar?
Passo 2
Vamos analisar o limite quando :
Como
Então,
Eu ouvi indeterminação ?! Eu ouvi L’Hôspital?!
Passo 3
Pronto! Para o numerador, usaremos a primeira parte do Teorema Fundamental do Cálculo.
Passo 4
O limite pode ser reescrito assim:
Agora é só substituir:
Resposta
Exercício Resolvido #2
UFF - Cálculo IIA - P1 Cristiane Argento 2012.2 - 2
Calcule o limite abaixo:
Passo 1
Huuum, misturou limite com integral... Já tá ligado no que vai acontecer, né? Não precisa ser nenhum mágico. Você vai cair numa indeterminação e vai ter que usar L’Hospital. Aí para derivar a função do numerador, vai ter que usar o Teorema Fundamental do Cálculo.
Vamos ver se acertamos?
Passo 2
Vamos analisar o limite quando :
Como
Então,
Uhuuul! L’Hôspital! L’Hôspital! (Todos vibram!)
Passo 3
Pronto! Para o numerador, usaremos o Teorema Fundamental do Cálculo.
Esse é aquele caso mais chatinho em que temos tanto o limite superior quanto inferior como funções de . Você lembra o que fazemos?
Primeiro, separamos os limites de integração:
Agora invertemos os limites de integração da primeira integral:
Passo 4
O denominador é fácil de derivar!
Passo 5
O limite pode ser reescrito assim:
Agora podemos substituir:
Resposta
Exercício Resolvido #3
USP - Cálculo 1 - P3 2009 -
Calcule o seguinte limite:
Passo 1
Não vou nem falar que isso aí tem aquela cara típica de problema que mistura Teorema Fundamental do Cálculo com limite para você não dizer que sou uma pessoa repetitiva.
Passo 2
Como sempre, temos que começar o limite substituindo o valor do :
Indeterminação de quociente, como dá para ver. O jeito mais prático de resolver é, como sempre, usar a Regra de L’Hospital, que consiste em derivar os termos de cima e de embaixo.
O detalhe é que temos que usar o Teorema Fundamental do Cálculo tanto em cima quanto embaixo, já que tanto o numerador quanto o numerador têm integrais.
Passo 3
Em ambos os casos, o limite superior é uma função de , então teremos que usar a regra da cadeia:
Pronto! Agora é só substituir e ser feliz!
Resposta
Exercício Resolvido #4
USP - Cálculo 1 - PREC 2015 - 1 b
Calcule os seguintes limites:
Passo 1
De novo temos uma questão em que ele pede para calcular o limite e no numerador e no denominador aparecem integrais. Então, mais uma vez, pequeno gafanhoto, acredito que você pode prever que você vai substituir o limite, cair numa indeterminação, aplicar L’Hospital e ter que usar o Teorema Fundamental do Cálculo para resolver!
Gente, esse pessoal de Cálculo I não tem criatividade, não?
Passo 2
Vamos substituir o valor do limite que aparece aí:
Isso significa que podemos usar nosso queridíssimo L’Hospital! Agora, para isso a gente tem que derivar usando o Teorema Fundamental do Cálculo.
Passo 3
Vamos começar derivando a função do numerador.
Opa! Parece que quem fez o enunciado colocou uma pimentinha para dar uma variada ali. Observa que no numerador desse quociente tem um termo dentro da integral que é função de . Como a integral é em podemos usar aquele macete de encarar esse é como se fosse uma constante e tirá-lo da integral:
Beleza. Aí você lembra que para derivar isso aí, temos que usar a regra do produto, né??
Só para ficar mais fácil se visualizar:
A derivada será dada por:
Que equivale a:
Passo 4
Agora vamos derivar a função do denominador
Observa que primeiro vamos ter que interver os limites te integração para poder aplicar o Teorema Fundamental do Cálculo:
Passo 5
Por L’Hospital, o limite pode ser reescrito como:
Agora podemos tentar substituir o limite:
Continuamos com indeterminação!
Passo 6
Como resolver essa indeterminação? Aplicando L’Hospital de novo:
É, digamos que não vai dar uma expressão muito bonita:
Eu sei, tá um monstro enorme. Agora, se substituirmos tudo que tem ou vai para , assim como o que é vai para e olha como vai ficar:
Resposta
Exercício Resolvido #5
Teorema Fundamental do Cálculo
Considere definida por . Na figura abaixo, representa a área da região indicada e é a área do triângulo com vértices em , e indicado.
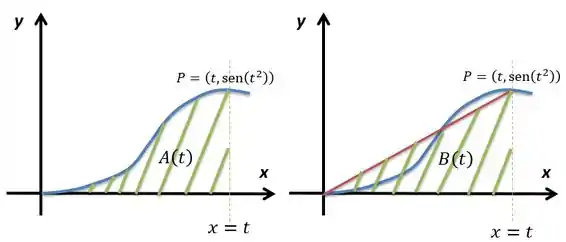
Determine .
Passo 1
Aeee. Finalmente uma questão diferentona!!
Vamos resolver essa questão com calma, começando primeiro definindo quem seriam esses e , porque só assim poderemos definir nossa estratégia de resolução, não é mesmo?
Segundo a primeira imagem, é a área de de até um ponto qualquer. Seria isso daqui:
Já o é simplesmente a área do triângulo com um vértice na origem, um em e outro em . Sua base é e sua altura é , então a área do triângulo será:
Assim, o limite que nos interessa é:
Passo 2
Bem, em tããão diferentona assim, né não?
Temos de novo aquela velha história de um limite misturado com uma integral. Como sempre, vamos substituir e ver o que acontece:
Já sabemos que integral com limites de integração iguais é nula. Então, adivinha? Caímos numa indeterminação do tipo:
Passo 3
Assim, como caímos numa indeterminação, podemos usar L’Hospital:
Bem, para o numerador, vamos usar o Teorema Fundamental do Cálculo; para o denominador usamos a Regra do Produto:
Passo 4
Vou calcular o inverso desse limite (deixando o de lado por enquanto) e depois eu desinverto o resultado e jogo nessa última expressão que achamos.
Vamos concentrar só nesse limite que sobrou:
Podemos usar L’Hospital nele, já que caímos em outra indeterminação:
Passo 5
Muita calma nessa hora pra não se confundir. Lembrando, vimos que a resposta da questão é:
Deixamos o 2 de lado, e focamos no limite
E a gente viu que o inverso desse limite é:
Ou seja, desinvertendo:
Agora é só multiplicar por 2 pra chegar na resposta final:
E essa é, finalmente, a nossa resposta! :)