Teoria
O que é antiderivada?
Se eu te pedir a derivada dessa função aqui:
Melzinho na chupeta né?
Mas e se eu te pedir uma função cuja derivada é ? Aí já complica um pouco. Aqui vamos ver como resolver esse tipo de problema.
Mas primeiro vamos dar nome aos bois. Basicamente, uma função é uma antiderivada ou primitiva de uma função em um intervalo qualquer se, para todo desse intervalo:
Ok, mas o que são integrais indefinidas?
A integral indefinida é uma notação usada para a primitiva. Escrevemos assim, ó:
Esse símbolo significa que estou procurando as antiderivadas ou a integral indefinida de .
Esse ali no fim é a constante de integração. Ele aparece porque a derivada de qualquer constante é zero, então:
Não se esqueça do !! Por causa dele, a integral indefinida de não é só uma função , e sim uma família de funções da forma , como a da foto aqui embaixo:

A única diferença entre as funções é o valor da constante, mas a derivada de todas elas é a mesma: .
Por isso há uma grande diferença entre integrais indefinidas e as definidas:
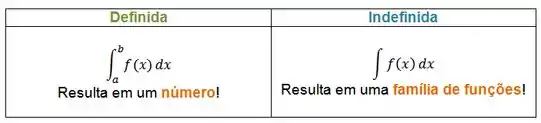
Agora vamos ver na prática como faz pra achar essas integrais!
Integrando funções trigonométricas
1)
(sou chato então vou relembrar: nunca, em hipótese alguma, esqueça a constante quando estiver trabalhando com uma integral indefinida!)
2)
3)
4)
5)
6)
Tem três que são um pouco mais difíceis de deduzir, mas que também são importantes de saber:
7)
8)
9)
Integrando polinômios
Detalhe que não precisa nem ser inteiro!
Só temos um caso especial, quando :
Integrando funções exponenciais
1)
2)
Integrando funções trigonométricas inversas
1)
2)
Pronto, chegamos ao fim! :)
E aí, pronto para treinar e não esquecer mais essas primitivas? Ó, e não vale fazer que nem o Pedrinho que decorou todas as primitivas mas esqueceu da constante!

Integrando funções trigonométricas
Integrando polinômios
Integrando funções exponenciais
Integrando funções trigonométricas inversas
Exercícios Resolvidos
Exercício Resolvido #1
PUC-RJ - Cálculo 1 - P3 2009.1 - 1a
Calcule:
Passo 1
Nessa questão, queremos resolver uma integral indefinida (observe a ausência de limites de integração).
Observe que a integral é formada por uma soma de funções, todas elas com integrais imediatas. É só utilizar as propriedades de integrais que já vimos e aquele resuminho de antiderivadas imediatas e TCHARANNN!
Passo 2
Já sabemos das propriedades de integrais que a integral da soma é igual à soma das integrais e que as constantes podem sair da integral. Logo, podemos reescrever a integral do enunciado como:
Passo 3
A primeira integral é uma integral de polinômio. Lembrando da regrinha de que integral de polinômio é dada somando ao expoente e dividindo por expoente :
Passo 4
A antiverivada ou integral de é . Portanto:
Passo 5
E a integral de é , então:
Passo 6
Juntando tudo:
A constante engloba as contantes anteriores.
Lembrando que você pode resolver essa integral em um único passo se se sentir seguro(a). Eu só dividi e fiz esse passo-a-passo para ficar bem mastigadinho e para você aproveitar e lembrar as propriedades, beleza? Na prática, quando cair no sangue, você vai resolver essa daí brincando!
Resposta
Exercício Resolvido #2
UFF - Cálculo IA – GMa – 2008.2 – Lista 18 – 11
Calcule a integral abaixo
Passo 1
Bem, de novo temos que pensar em transformar esse troço aí em algo que sabemos resolver com integrais imediatas. Huuum... tem uma diferença de exponenciais em cima e apenas uma exponencial. E a função tem uma integral imediata.
Não parece que essa função está pedindo uma divisão básica do numerador pelo denominador?
Passo 2
Até porque, para dividir isso aí, é só lembrar da regrinha de divisão de expoentes com a mesma base, né?
Parece que conhecemos as duas integrais ali que sobraram, né? A integral de e a integral de (Lembra que esse aí é uma constante, que é o mesmo que um polinômio , beleza?
Então é só mandar ver (lembra de colocar a constantezinha esperta, claro!)
E acabou!
Resposta
Exercício Resolvido #3
James Stewart, Cálculo Vol. 1, 6ª ed. São Paulo: Cengage Learning, 2010, pp 373 - 16
Ache a integral indefinida geral.
Passo 1
O enunciado nos pede para calcularmos a integral indefinida.
Várias funções trigonométricas têm integrais imediatas. Então ao invés de se desesperar, que tal tentar manipular essa expressão ninjamente para chegar nessas integrais imediatas? (Na real, nem precisa ser ninja, vai, aquela ali do lado de fora está pedindo, muito forte, para você fazer uma distruibutiva!)
Passo 2
Vamos aplicar a distributiva:
Passo 3
Ficou mole! Lembra?
Passo 4
É só juntar e correr pro abraço:
Resposta
Exercício Resolvido #4
UFF - Cálculo IA – GMa – 2008.2 – Lista 18 – 11
Calcule a integral abaixo
Passo 1
Huum, de novo vamos pensar em transformar essa joça em algo que sabemos resolver com integrais imediatas.
Observa que o termo dentro da raiz é igualzinho ao termo que aparece no denominador? Se lembramos que acho que fica mais fácil de visualizar que podemos dividir o numerador pelo denominador , não é mesmo?
Passo 2
Assim, olha o que eu vou fazer:
Agora temos . Se voltarmos para a forma de raiz:
Passo 3
E aí? Lembrou que a temos uma integral direta para essa função de ? Talvez você não lembre, mas essa integral cai na definição da derivada de . E é isso, nada mais a ser feito (pode estar parecendo mágica demais, mas o objetivo dessas questões é justamente que você tenha memorizado essas primitivas).
Ahh, só para não perder o costume: não esquece !
Resposta
Exercício Resolvido #5
UFF - Cálculo IA – GMa – 2008.2 – Lista 18 – 11
Calcule a integral abaixo
Passo 1
Novamente temos uma integral indefinida para resolver. A princípio, ela não parece imediata. Mas podemos facilmente transformá-la em uma integral formada por uma soma de funções que têm integrais imediatas. Quer ver?
Passo 2
É só lembrar que é o mesmo que .
Aí, se usarmos a propriedade distributiva, olha que lindo:
Repara que agora temos apenas polinômios! Basta integrar segundo a primitiva dos polinômios. Ouvi dizer que você já está craque na regrinha para integrar polinômios (Shhh... prometo não contar seu segredo para ninguém, pequeno(a) nerd!).
Ah, e não esquece aquela constante esperta para indicar a família, ok?
Sinta-se orgulhoso(a)! Com regrinhas simples você já sabe integrar várias funções. Tirou onda agora, hein?
Resposta
Exercício Resolvido #6
PUC-RJ - Cálculo B - P1 2012.1 - 2 d
Calcule as integrais:
Passo 1
Bem, temos que resolver essa integral indefinida aí em cima. Considerando que só sabemos integrais imediatas, porque ainda não aprendemos nenhum método de integração mirabolante, precisamos encontrar uma forma de fazer isso aí ficar com cara de algo que a gente saiba resolver.
Passo 2
Pensa bem: essa integral é formada apenas por polinômios. Ora, se nós abrirmos o polinômio e depois dividirmos cada termo por nós teremos apenas potências de , o que significa que conseguiríamos resolver tudo através de integrais de polinômio.
Lembrando que e que 9 é o mesmo que :
Agora é só integrar, lembrando da regra de derivação de polinômios e sem esquecer da constante de integração, hein??
Se quisermos deixar mais bonitinho, podemos colocar e em evidência: