Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.1 - Ex. 45
Encontre o domínio e esboce o gráfico da função.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado quer que a gente esboce o gráfico e encontre o domínio da seguinte função:
Isso significa que vamos ter que determinar os valores de para os quais a nossa função está definida.
Só que é mais fácil pensar em quais valores de a função não pode assumir, por isso procuramos sempre por restrições para definir o domínio de uma função. Se ela não tiver nenhuma restrição, seu domínio será todo o conjunto dos números reais.
Dessa forma, vamos sempre analisar se existem valores que deixem um denominador igual a zero ou que façam uma raiz de índice par ter o radicando negativo, por exemplo.
Observe que a nossa função tem um módulo, então vamos precisar usar a definição de função modular para encontrar as restrições dela e, em seguida, esboçar nosso gráfico.
Vamos lá!
Passo 2
Como a nossa função tem um módulo, vamos começar pescando a definição de módulo:
Agora, que tal somar dos dois lados da equação? Olha só como fica:
Dividindo todo mundo agora por , temos:
Agora temos a nossa função do lado esquerdo da equação, então encontramos uma definição pra ela do lado direito.
Nota uma coisa importantíssima agora! Se eu dividi por , então eu tenho que transformar em ! Afinal, não posso dividir nada por zero! Vemos então que nessa função, o zero não está definido! Cortando os nas definições (simplificando), chegamos a:
Logo,
Passo 3
E esse é o nosso último passo galera! Como:
Temos uma constante se for maior do que zero e outra constante se for menor do que zero. Dessa forma, nosso gráfico fica assim:
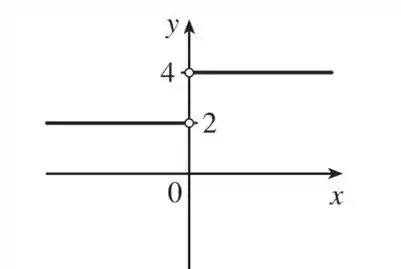
E essa bolinha branca é bem importante viu? Ela mostra que nem é igual a e nem igual a ! Afinal, é indefinido! Pra qualquer outro valor de , a função ou assume o valor ou o . Portanto o nosso domínio são todos os números reais, exceto o zero, ou seja:
Ou, na notação de intervalo:
Valeu, galera! Até a próxima! 😉