Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.2 - Ex. 18
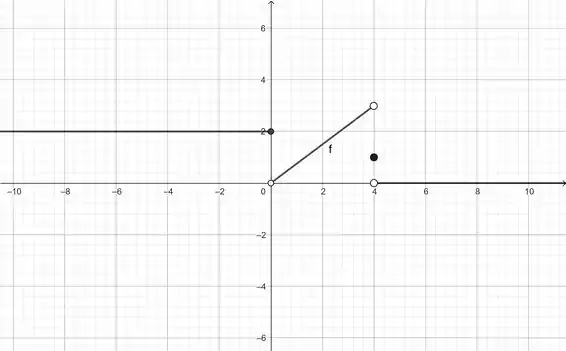
2.18. Esboce o gráfico de um exemplo de uma função que satisfaça a todas as condições dadas.
Passo 1
Eaeee, belezinha?? Bom... a questão nos deu os seguintes limites de uma função :
E esses dois pontos:
Com essas informações queremos esboçar o gráfico de uma função que satisfaça a todas as condições dadas.
Para isso, temos que interpretar cada informação dessa.
E aí?? Bora lá?? 😉
Então, pessoal, uma dica para esse tipo de questão é: comece sempre marcando no gráfico a bolinha cheia onde você a sabe que a função é definida naquele ponto.
Neste caso, a gente começa marcando onde estão: e.
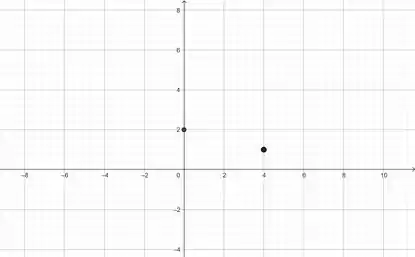
Feito isso, a gente olha para os limites!
Aí é só desenha uma função que leve para onde o limite indica, mas marcá-la com a bolinha vazia, caso a função exista em outro ponto.
Vamos lá!
Passo 2
No ponto , quando olhamos pelos valores que se aproximam pela esquerda, temos:
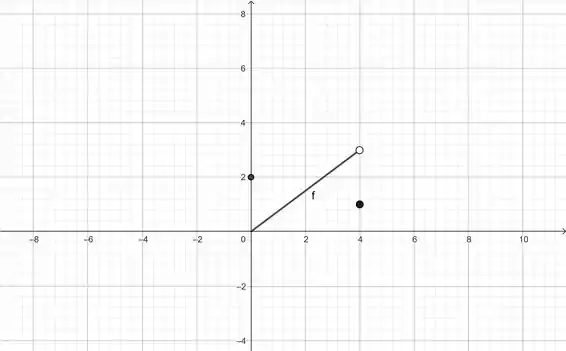
Que significa que a função tende a .
Por outro lado, olhando para os valores que se aproximam pela direita, temos:
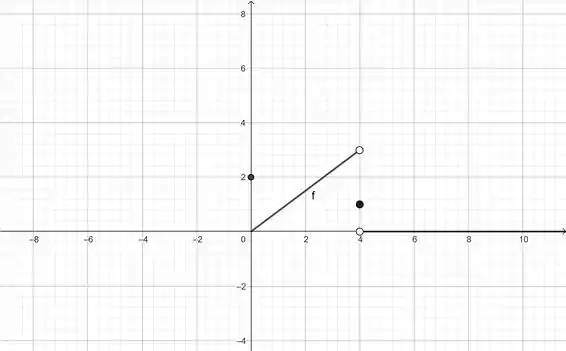
Que significa que a função tende a .
Passo 3
Ainda temos esses dois limites:
Isso quer dizer que quando se aproxima de zero pela esquerda, a função tende a .
Por outro lado, quando se aproxima de zero pela direita, a função tende a zero!!
Com essas informações, o gráfico vai ficar o seguinte:
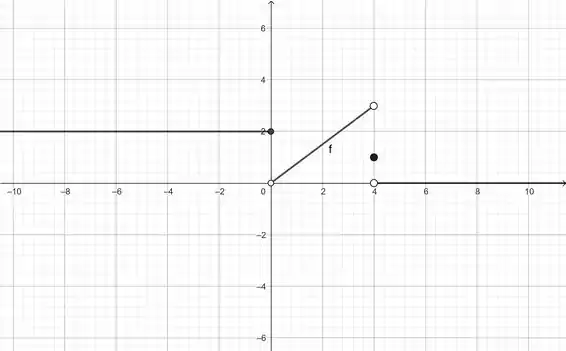
Lembrando que as bolinhas preenchidas significam que o ponto pertence a função, e as bolinhas que não estão preenchidas, significa que o ponto não está na função.
Resposta
