Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.1 - Ex. 45
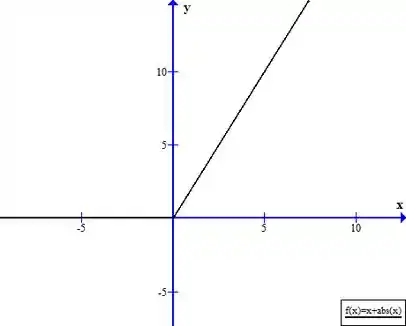
Esboce o gráfico da função
Passo 1
Eaeee, belezinha? Bom... a questão quer que esbocemos o gráfico da seguinte função:
Para isso, temos que analisar bem o comportamento da nossa função. Muito geral isso, né?? Mas vamos com calma...
A gente pode reparar a princípio que temos um módulo nesta função.
E aqui vale lembrar que a função módulo nada mais é que uma função definida por partes:
Com isso, podemos inferir que a função módulo é puramente quando é positivo, e ela é quando é negativo (faz sentido né, dessa forma ela transforma o número negativo em um positivo).
Vamos ver com mais detalhes?? 😉
Passo 2
Então quando for qualquer valor positivo, o módulo não faz qualquer diferença na função, e pode ser tirado, ficando:
Agora, quando possui valores negativos, então a gente coloca um símbolo de negativo na frente do . Veja só:
Então, vemos que quando for negativo, a função sempre será nula. Faz sentido, não?
Passo 3
Agora vamos traçar o gráfico.
Para :
temos uma linha horizontal em .
E para :
temos uma reta do tipo .
Para traçar a reta, basta dois pontos quaisquer.
Quando , temos:
Quando , temos:
Nossa função é a linha em preto.
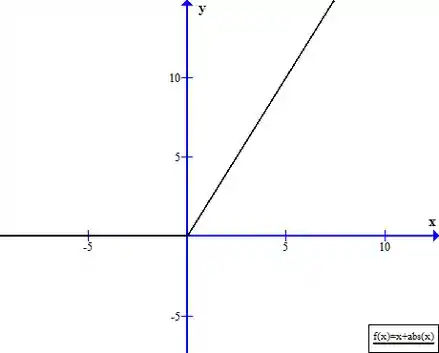
Resposta
