23. O movimento de determinado pêndulo não amortecido é descrito pelas equações
Se o pêndulo for colocado em movimento com um deslocamento angular e sem velocidade inicial, então as condições iniciais serão .
(a) Considere e faça o gráfico de x em função de t. Do gráfico, estime a amplitude R e o período T do movimento resultante do pêndulo.
(b) Repita o item (a) para
(c) De que modo a amplitude e o período do movimento do pêndulo dependem da posição inicial ? Desenhe um gráfico para mostrar cada uma dessas relações. Você pode dizer alguma coisa sobre o valor limite do período quando ?
(d) Seja e faça o gráfico de x em função de t. Explique por que esse gráfico difere dos gráficos nos itens (a) e (b). Para que valor de ocorre a mudança?
Passo 1
Bem, essa questão nos permite a ajuda de um computador, então vamos lá! Se aqui utilizarmos a ajuda do WOLFRAMALPHA, um site muito esperto que realiza muitos cálculos de graça pra gente, e digitarmos essa equação do jeitinho que está aqui na barrinha:
Ele vai resolver esse sistema pra gente encontrando o seguinte campo de vetores:
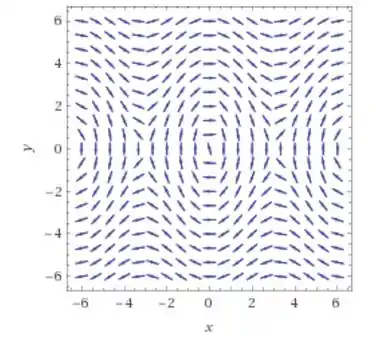
Repare então que até mais ou menos a gente pode aproximar o nosso sistema por EDO’s linear ao redor de . Na letra D, entretanto, que nos pede ao redor de , temos que encontrar outro ponto critico para aproximar que não será o .
Passo 2
Então a primeira coisa a se fazer nesse problema é aproximar a EDO não linear por uma EDO linear conveniente. Para isso...
Primeiro devemos encontrar os pontos crítico desse sistema de EDO:
Ponto crítico acontece quando a derivada é , ou seja:
Um ponto que a gente já consegue ver que é ponto crítico é o e :
Mas esse não é o único ponto crítico! Todos os pontos que tornam o , são pontos críticos. No caso...
Veja que o nosso ponto e encontrado, também faz parte desse conjunto, pasta tomar :
Resumindo: temos vários pontos críticos, mas apenas três são relevantes:
O é para a aproximação das condições pedidas no item A e B, e o ponto será ponto que vamos usar para aproximar para a letra D já que pela figura dá para ver que está mais próximo de do que de , saca?
Passo 3
A primeira coisa para determinar um sistema linear próximo a um ponto crítico é pegar a o sistema que estamos trabalhando:
E chamar...
Agora, dessas duas funções aí, e , devemos extrair a matriz Jacobiana dada por:
Calculando essas derivadas parciais então...
Beleza! Agora temos que substituir os nossos pontos críticos. Como são dois, vou fazer isso em dois passos extras, ok?
Passo 4
Primero o do ponto , isto é:
Como o cosseno de é ...
De acordo com a teoria, o sistema de EDO linear que aproxima a não linear nesse caso é:
é o e o .
Para o ponto no qual vamos aproximar a letra D:
A aproximação linear que vamos fazer aqui será então...
Passo 5
Como vimos, precisamos para a o item de A a C nos aproximar da EDO:
Como o exercício nos permite agilizar a nossa vida com um computador, usando o Wolframalpha e resolvendo esse sistema linear, vamos obter...
Substituindo as condições iniciais do nosso problema: ...
Então...
Desenhando isso no plano ...
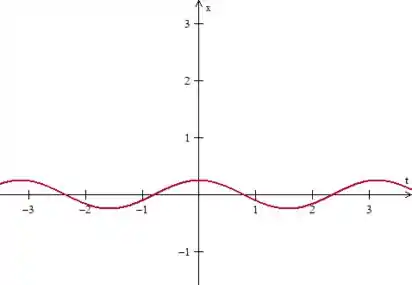
A amplitude aproximada aqui é e o período vem de ...
Passo 6
Usando as mesmas equações:
Só que trocando agora e ...
Ou seja, a solução agora será...
A amplitude da nossa EDO não linear então que descreve o movimento do pêndulo será e :
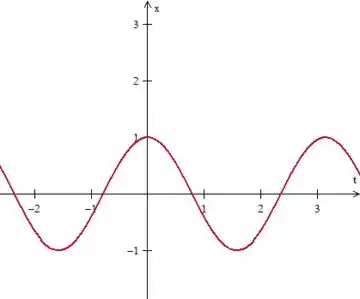
Passo 7
Repare então que a única diferença e o que muda é a amplitude que dependerá de . No geral, podemos falar que:
Então se ...
Se ...
E se ...
A as amplitudes então será: respectivamente. O período será o mesmo para todas elas e é de . A curva vai ser a mesma senoidal só que com amplitudes diferentes, saca?
Passo 8
Como vimos, o período depende diretamente do valor de :
De modo que se A varia, varia linearmente:
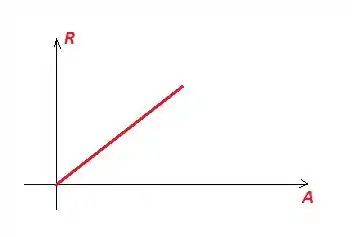
Podemos dizer que se fizermos , teremos uma amplitude de (uma linha):
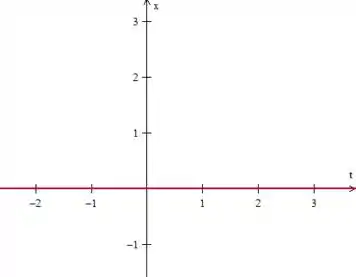
Passo 9
Como vimos, o é o único nesse caso que não podemos aproximar pela solução daquela EDO linear que encontramos no passo 4. Temos então que nos aproximar pela solução dessa EDO aqui:
Jogando então no WOLFRAMALPHA, obteremos:
Substituindo a condição inicial indicada nesse item: e ...
E...
Ou seja...
E a solução então será...
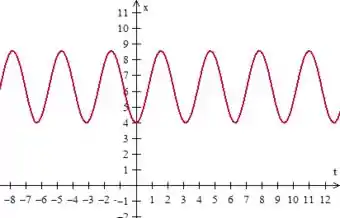
A amplitude dessa onda agora será de , mas o período continua o mesmo :
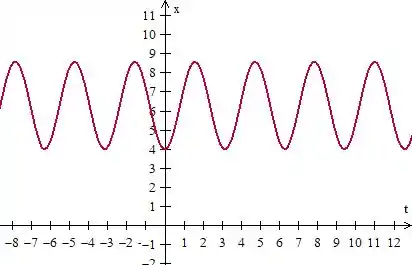
Ele se difere dos outros, simplesmente por causa de ser um ponto que já está mais próximo de , o qual vimos ser um ponto crítico para a EDO não linear.
Se lembra desse ponto crítico aqui: ?
Então, esse ponto é o que separa as duas aproximações! Qualquer deve ser aproximado pela primeira e deve ser aproximado por essa segunda, saca?
Resposta
Letra A: e . Gráfico de uma cossenoide.
Letra B: e para todas elas. Gráfico de uma cossenoide.
Letra C: . Relação linear. é uma reta no gráfico .
Letra D: