Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 9.3 - Ex. 29

Neste problema, vamos deduzir uma fórmula para o período natural de um pêndulo não linear não amortecido [ c   =   0 na Eq. (10) da Seção 9.2]. Suponha que a massa é puxada por um ângulo positivo α e depois é solta com velocidade zero.

(a) Pensamos, em geral, em θ e d θ / d t como funções de   t . No entanto, invertendo os papéis de t e θ, podemos considerar t como função de   θ e, portanto, pensar, também, em d θ / d t como função de θ . Deduzimos, então, a seguinte sequência de equações:

1 2 m L 2 d d θ d θ d t 2 = - m g L sin ⁡ θ

1 2 m L 2 d d θ d θ d t 2 = m g L cos ⁡ θ - cos ⁡ α

d t = - L 2 q d θ cos ⁡ θ - cos ⁡ α

Por que foi escolhida a raiz quadrada negativa na última equação?

(b) Supondo que T é o período natural de oscilação, deduza a fórmula

T 4 = - L 2 q ∫ α 0 d θ cos ⁡ θ - cos ⁡ α

(c) Usando as identidades cos ⁡ θ = 1 - 2 sin 2 ⁡ ( θ / 2 ) e cos ⁡ α = 1 - 2 sin 2 ⁡ α / 2 , seguidas pela mudança de variável s e n ( θ / 2 )   =   k   s e n ϕ , com k   =   s e n ( α / 2 ) , mostre que

T = 4 L q ∫ 0 π / 2 d ϕ 1 - k 2 sin 2 ⁡ ϕ

Essa é uma integral elíptica de primeira espécie. Note que o período depende da razão L/g e, também, do deslocamento inicial α , através de k   =   s e n ( α / 2 ) .

(d) Calculando a integral na expressão para T, obtenha valores de T que você possa comparar com as estimativas gráficas obtidas no Problema 23.

Passo 1

Que tal começarmos esse problema desenhando esse pendulo só pra gente ter uma noção de como resolver?

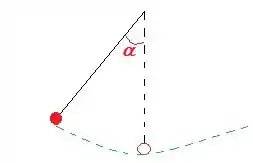
Beleza! Então agora podemos começar! Bora?

Passo 2

L e t r a   A :

Bem, repare que a nossa bolinha vermelha está saindo de uma posição angular α no tempo t = 0 e indo para a posição 0 (pendulo pontilhado para baixo).

Então se estamos falando de t θ , a medida que o tempo avança de 0 o ângulo θ sai da posição α e começa a ir para o ângulo 0 , indicando que t e θ devem ter sentidos opostos, saca? Por isso o sinal de fato deve ser negativo .

Passo 3

L e t r a   B :

Repare que chamamos de período o tempo T levado para a bola sair da posição dela e voltar para a mesma posição de onde ela deixou fazendo uma volta completa, saca?

Então, para a bola sair dessa posição angular α :

E chegar ao ângulo 0 , ela vai levar 1 / 4 do tempo de um período T .

O ângulo θ por sua vez está variando de α até 0 , então...

d t = - L 2 q d θ cos ⁡ θ - cos ⁡ α   →

Integrando dos dois lados...

∫ 0 T 4 d t = - ∫ α 0 L 2 q d θ cos ⁡ θ - cos ⁡ α     →

T 4 - 0 = - L 2 q ∫ α 0 d θ cos ⁡ θ - cos ⁡ α     →

T 4 = - L 2 q ∫ α 0 d θ cos ⁡ θ - cos ⁡ α

VIU SÓ!

Passo 4

L e t r a   C :

Vamos fazer aqui como ele nos sugeriu, ou seja, pegando a nossa integral...

T 4 = - L 2 q ∫ α 0 d θ cos ⁡ θ - cos ⁡ α

E trocando cos ⁡ θ = 1 - 2 sin 2 ⁡ ( θ / 2 ) e cos ⁡ α = 1 - 2 sin 2 ⁡ α / 2 , :

T 4 = - L 2 q ∫ α 0 d θ 1 - 2 sin 2 ⁡ θ 2 - 1 - 2 sin 2 ⁡ α 2       →

T = - 4 L 2 q ∫ α 0 d θ - 2 sin 2 ⁡ θ 2 + 2 sin 2 ⁡ α 2    

Fazendo a mudança de variável então sugerida...

sin ⁡ θ 2 =   k sin ⁡ ϕ

Não se esqueça de derivar implicitamente em relação a ϕ heim!

cos ⁡ θ 2 ⋅ 1 2 d θ d ϕ = k cos ⁡ ϕ     →

Lembre-se de que cos ⁡ θ 2 = 1 - sin 2 ⁡ θ 2   :

d θ = 2 k cos ⁡ ϕ 1 - sin 2 ⁡ ( θ / 2 ) d ϕ   →

d θ = 2 k cos ⁡ ϕ 1 - k 2 sin 2 ⁡ ϕ d ϕ

Onde...

k   = sin ⁡ α 2

Então pela nosso mudança...

sin ⁡ θ 2 =   k sin ⁡ ϕ

sin ⁡ θ 2 = sin ⁡ α 2 sin ⁡ ϕ       →

Podemos agora encontrar os novos limites de integração substituindo os antigos: θ = α e θ = 0 :

θ = α       →             sin ⁡ α 2 = sin ⁡ α 2 sin ⁡ ϕ   →                 sin ⁡ ϕ = 1     →               ϕ = π 2

θ = 0       →             sin ⁡ 0 = sin ⁡ α 2 sin ⁡ ϕ   →               sin ⁡ ϕ = 0             →                     ϕ = 0

Com isso tudo em mãos, podemos retornar para a integral que estamos querendo encontrar:

T = - 4 L 2 q ∫ α 0 d θ - 2 sin 2 ⁡ θ 2 + 2 sin 2 ⁡ α 2     →

E substituir todo mundo (não se esqueça dos limites também):

T = - 4 L 2 q ∫ π 2 0 2 k cos ⁡ ϕ 1 - k 2 sin 2 ⁡ ϕ d ϕ - 2 k sin ⁡ ϕ 2 + 2 k 2       →

Simplificando um pouquinho essa integral...

T = 4 L 2 q ∫ 0 π 2 2 k cos ⁡ ϕ 1 - k 2 sin 2 ⁡ ϕ ⋅ - 2 k 2 sin 2 ⁡ ϕ + 2 k 2 d ϕ       →

T = 4 L 2 q ∫ 0 π 2 2 k cos ⁡ ϕ 1 - k 2 sin 2 ⁡ ϕ ⋅ 2 k 2 1 - sin 2 ⁡ ϕ d ϕ       →

Novamente se recordando que 1 - sin 2 ⁡ ϕ = cos ⁡ ϕ pela relação fundamental da trigonometria...

T = 4 L 2 q ∫ 0 π 2 2 k cos ⁡ ϕ 1 - k 2 sin 2 ⁡ ϕ ⋅ 2 k cos ⁡ ϕ d ϕ       →

T = 4 L 2 q ∫ 0 π 2 2 1 - k 2 sin 2 ⁡ ϕ d ϕ       →

T = 4 L q ∫ 0 π 2 1 1 - k 2 sin 2 ⁡ ϕ d ϕ    

PRONTINHO!

Passo 5

L e t r a   D :

De fato trata-se de uma integral elíptica do primeiro tipo. Usando o WOLFRAMALPHA para integrar e encontrar a resposta, vamos obter:

T = 4 L q ⋅ K k 2 k 2 - 1 1 - k 2

Onde K m é a integral elíptica!

Resposta

T = 4 L q ⋅ K k 2 k 2 - 1 1 - k 2

Onde K m é a integral elíptica tipo 1.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o ponto de bifurcação α0 no qual os pontos críticos coincidem. Localize esse ponto crítico e encontre os autovalores do sistema linear aproximado. Desenhe um retrato de fase..
Seja α = 2. Classifique cada ponto crítico investigando o sistema linear correspondente. Desenhe um retrato de fase em um retângulo contendo os pontos críticos..
Para αα0 não existem pontos críticos. Escolha um desses valores de α e desenhe um retrato de fase..
Desenhe retratos de fase para o sistema para valores selecionados de α para confirmar suas conclusões.
Encontre os pontos críticos.