32. O gráfico da Figura 2.11 ilustra a propragação de uma epidemia numa cidade X. No eixo horizontal temos o tempo e no eixo vertical, o número de pessoas atingidas depois de um tempo (medido em dias a partir do primeiro dia da epidemia).

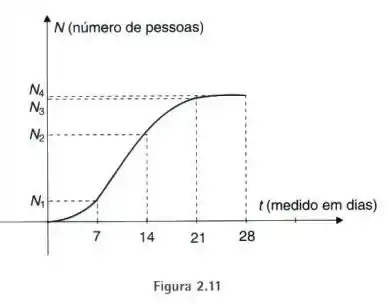
1. Em qual semana houve o maior número de pessoas infectadas?
2. Quando a epidemia foi totalmente controlada?
3. Como você descreveria a propagação da doença em linguagem coloquial?

(a)

A primeira pergunta é em qual semana houve um maior número de infectados, em termos dos gráficos. A pergunta seria assim: Em qual semana houve um maior crescimento, ou seja, qual ficou mais inclinada?

Ora, olhando para o gráfico, isso ocorre na segunda semana!!

(b)

Agora, vamos para a segunda pergunta! A pergunta é: Quando a epidemia foi controlada?

Em termos do gráfico, a pergunta seria assim: Quando que o gráfico da epidemia fica constante!

O gráfico fica quase constante na semana, ou seja, a epidemia está controlada na semana.

1. No começo, não temos quase ninguém afetado e começa a crescer devagar até a semana! Depois vem um surto da doença na semana, quando muitas pessoas são afetadas, o ritmo diminui até a terceira semana e já na quarta semana há um controle da epidemia!