Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 34

Defina uma função inversa para y = cosh ⁡ x , para x ≤ 0 . Esboce o gráfico.

Passo 1

Bom, galera, vamos dar uma olhada no gráfico da função cosseno hiperbólico para x ≤ 0 .

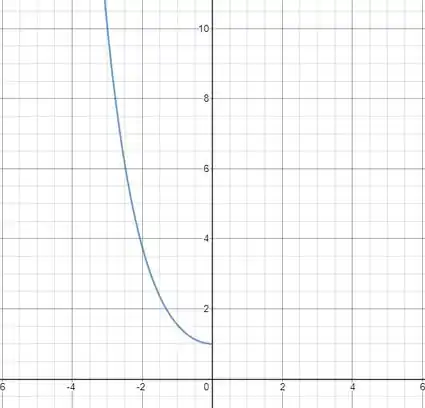
Aqui temos que f : - ∞ , 0 → [ 1 , + ∞ ) . Portanto, a sua inversa será uma função f - 1 : 1 , + ∞ → ( - ∞ , 0 ] . Usando que x = cosh ⁡ y = e y + e - y 2 , podemos escrever

2 x = e y + e - y

e y - 2 x + e - y = 0

e 2 y - 2 x e y + 1 = 0

Passo 2

Vamos fazer uma substituição de variáveis aqui. Seja a = e y . Assim, nossa equação se torna:

a 2 - 2 x a + 1 = 0

Resolvendo essa equação de segundo grau, temos:

a = 2 x ± 4 x 2 - 4 2

Voltando para a variável original:

e y = 2 x ± 4 x 2 - 4 2 = x ± x 2 - 1

Como y ∈ ( - ∞ , 0 ) , temos que 0 < e y < 1 . Portanto, vamos usar o sinal negativo aqui, o que nos leva a ter

e y = x - x 2 - 1

Aplicando o logaritmo natural dos dois lados da equação, temos:

y = ln ⁡ x - x 2 - 1

A figura a seguir mostra o gráfico da função inversa

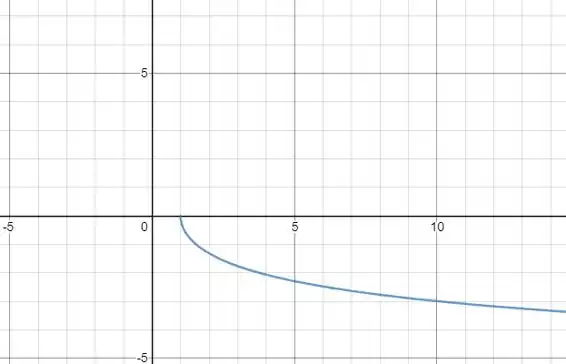
Resposta

A função inversa é:

y = ln ⁡ x - x 2 - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é o período das seguintes funções reais: b) f (x) = (1 - t g^2 2 x)/(1 + t g^2 2 x)
Qual é o período das seguintes funções reais: c) h (x) = cos^6 x + s e n^6 x
Qual é o período da função dada por f (x) = (1 + cos 4 x)^((1)/(2))
Estude a variação da função f (x) = (1 - cos 2 x)^((1)/(2)) * (1 + cos 2 x)^(- (1)/(2))
Qual é o período da função f (x) = (1 + t g x)/(1 - t g x) ?