Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 35
Calcule a integral, interpretando-a em termos das áreas.
Passo 1
Faala ae, beleza?? Yuri aqui e nessa questão vamos calcular a integral abaixo, só que como uma interpretação mais geométrica:
O enunciado pede pra a gente interpretar essa integral em termos de área.
Sabemos que a integral representa a área entre a função e o eixo . Se a função está acima do eixo , a integral é o valor da área puramente, e se a função está abaixo do eixo , a integral é o valor da área só que negativo.
Precisaremos portanto ter uma ideia do gráfico dessa função. Para isso, podemos pensa-la como uma função reta (função afim) ou usar a função que possui gráfico conhecido e fazer algumas operações gráficas até obter o gráfico de .
Passo 2
Encontrando o gráfico da função , vemos que ela é uma função afim (isso é, ela é uma reta):
Onde é o ponto onde a reta cruza o eixo .
Para traçar uma reta só precisamos de dois pontos.
Usando por exemplo teremos:
Dessa forma, sabemos que nossa reta passa pelos pontos:
Com isso, nos resta apenas o gráfico abaixo:
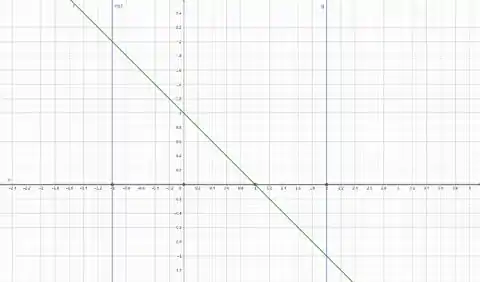
A definição de integral é justamente a área sobre a curva, mas nesse caso temos duas áreas, uma acima de e outra abaixo.
Passo 3
Uma outra forma de obter o gráfico do Passo 2, é através de operações gráficas.
Conhecemos o gráfico de , ele é uma reta de com a horizontal que passa na origem.
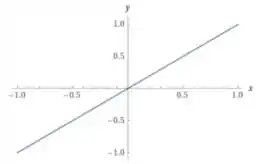
O gráfico de é esse mesmo gráfico mas refletido ao redor do eixo :
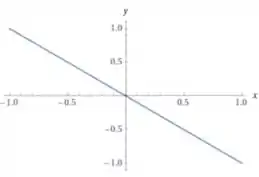
E por fim o gráfico de , é o gráfico de transladado em uma unidade para cima.
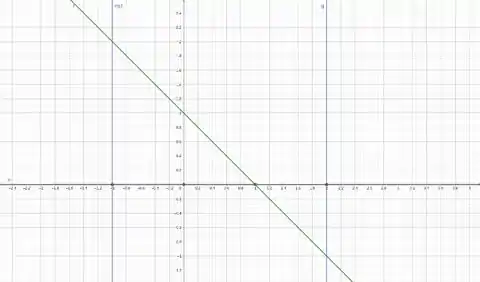
Passo 4
Para calcular aqui nossa área, iremos utilizar a fórmula da área de um triangulo:
Como temos 2 triângulos e um deles está abaixo de , está área será subtraída: