Calcule a integral, interpretando-a em termo de áreas.

Olá, amigo. Yuri aqui e estarei te ajudando a resolver essa atividade de integral. Nos é pedido para que calculemos a integra utilizando os conceitos de área. Então é isso que iremos fazer

Vamos ter que fazer o gráfico da função . Já que temos que interpretar em termos de áreas, nada mais justo que analisar o gráfico.

Com o auxílio do GeoGebra:

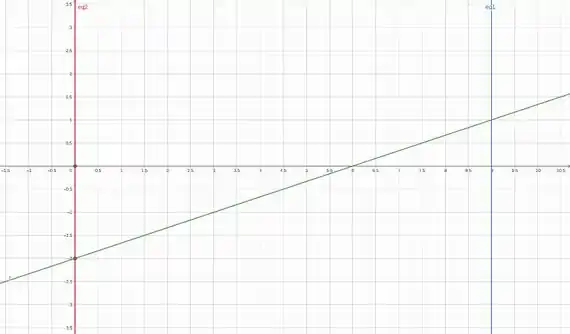
Olhando bem dá pra ver dois triângulos retângulos, então calcular a área da função, nada mais é que a gente encontrar a área do triângulo da parte positiva e subtrair do da negativa. Ou seja, a área corresponde a uma diferença de áreas de dois triângulos.

Vamos para as contas, então!