Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 36
36. Um pacote de suprimentos médicos de um helicóptero diretamente para baixo de paraquedas em uma área remota A velocidade do pacote segundos após começar a cair é dada em pés por segundo por .
- Faça o gráfico de .
- Mostre que o gráfico tem uma assíntota horizontal .
- A constante é denominada . Explique qual o sentido prático dela.
- O pacote pode realmente atingir sua velocidade terminal? Explique.
- Quanto tempo leva para o pacote atingir de sua velocidade terminal?
Passo 1
Belezoca galera, o gráfico da função é:
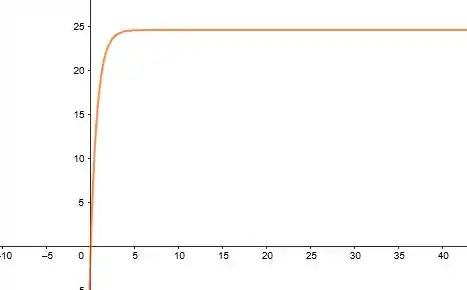
E como a letra (b) nos disse, temos de fato uma assíntota em . Que é o nosso coeficiente que está multiplicando toda função, logo esse coeficiente que restringe esse limite da função.
Passo 2
Essa constante é denominada velocidade terminal e na prática isso quer dizer que ela é o limite da velocidade que o objeto pode alcançar, isto é, para o nosso caso onde , a velocidade terminal é exatamente essa.
E teoricamente o pacote atinge a velocidade, mas na prática isso aconteceria somente em , ou seja, ele ia precisar cair pra sempre pra cogitar atingir a velocidade terminal.
Passo 3
Por exemplo, na letra (c), vamos calcular o tempo que ele leva para chegar em da velocidade terminal. Se a terminal vale , disso, fazendo rapidinho aqui pra vocês, valem:
Logo, queremos a igualdade:
Então isolando o temos:
E agora tirando o sinal de negativo da nossa exponencial, temos:
Tirando a exponencial, chegamos em:
Resposta
-
- Explicação.