24. A resistência elétrica em para um fio de metal puro está relacionada com sua temperatura em pela fórmula:
Na qual e são constantes positivas.
- Faça um esboço á mão do gráfico de versus e explique o significado geométrico de e para seu gráfico.
- Em teoria, a resistência de um fio de metal puro cai para zero quando a temperatura atinge zero absoluto . Que informação isso fornece sobre ?
- Uma lâmpada com filamento de tungstênio tem uma resistência de a uma temperatura de . Que informação isso fornece sobre o do filamento?
Passo 1
Belezoca galerinha, como aqui não podemos fazer o gráfico a mão, primeiro vamos entender o significado geométrico de e . Saca só, o enunciado disse pra gente que a equação que relaciona essas grandezas é:
E queremos analisar o significado de e no gráfico dessa função de versus . Então vamos testar algumas coisas. Por exemplo, se a temperatura for igual a , teríamos:
Ou seja, quando a temperatura em é igual a , a resistência elétrica do nosso fio de metal é igual a resistência “inicial” . Então podemos assumir também que o gráfico cruza o eixo R em , isto é, em .

Iradoso, agora que a gente entendeu o significado de , podemos passar pro . Se liga só, na fórmula , o nosso está multiplicando a temperatura . Ou seja, quanto maior o valor de , maior será a resistência elétrica enquanto a temperatura estiver subindo.
Se aplicássemos a distributiva dentro desse produto, teríamos:
E essa família de curvas pertence as equações de primeiro grau, onde o é o coeficiente angular da reta, e esse coeficiente angular é quem dita o crescimento da reta. Em outras palavras, quanto maior esse coeficiente, mais inclinada será reta. Então para um reta qualquer, do tipo:
Podemos garantir, que ela cruza o eixo em e a inclinação da reta é igual .
Então supondo os valores de e , uma reta que satisfaz a equação é:
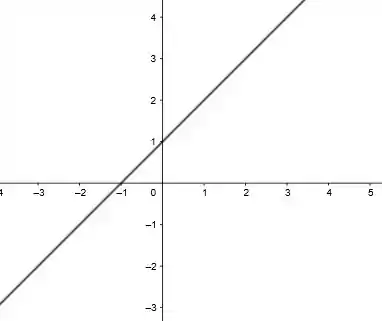
Passo 2
Na letra (b), se temos então:
E ele diz que a essa temperatura, a resistência elétrica é igual a , logo:

Passo 3
E na letra (c), se tivermos e , então:
Resposta
- Demonstração.