Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.1 - Ex. 37
37-38 Estime o valor de dando um zoom no gráfico de . Depois derive a e determine o valor exato de e compare com a sua estimativa.
37.
Passo 1
Fala aí, tudo belezinha com você?
Bom, essa questão pediu pra gente dar um zoom no gráfico da função
Para estimar o valor de , sendo .
E depois disso, determinar o valor exato de , derivando a função no ponto , para então, comparar os dois resultados e ver se nossa estimativa foi boa.
Vamos então começar traçando o gráfico da função e lembrando que a derivada da função em um ponto pode ser entendida como a inclinação da reta tangente ao gráfico da função naquele ponto.
Assim, basta traçar também a reta tangente ao gráfico da função no ponto pedido e calcular seu coeficiente angular. Lembrando que:
Depois disso, vamos derivar, de fato, a função e comparar como o resultado obtido anteriormente.
Vamos nessa!
Passo 2
Começamos desenhando o gráfico da função
Sendo:
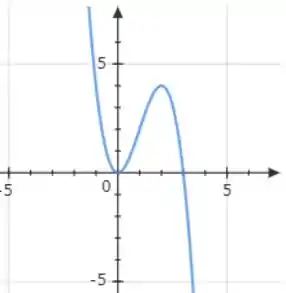
Agora vamos dar um zoom no ponto
Faremos primeiramente o gráfico de
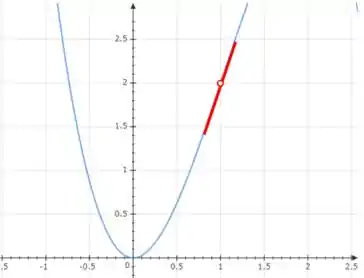
Vamos traçar um triângulo retângulo para determinar o coeficiente angular da nossa reta. Observe:
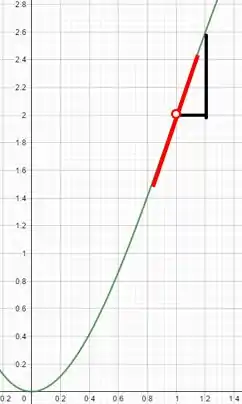
Lembrando que:
E considerando e
Teremos:
É aproximado, pois não conseguiríamos traçar certinha a reta!
Passo 3
Agora faremos a derivada da função para poder comparar com o que já temos. Assim:
Aplicando a regra de derivação em cada termo, ficamos com:
Assim, nossa derivada se torna:
Passo 4
Agora substituirmos o valor de para acharmos o valor de .
Que é igual ao que estimamos no gráfico!!
E prontinho! Questão resolvida.