Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.5 - Ex. 51
Ache uma equação de reta tangente ao gráfico da função seno no ponto
Passo 1
Bom, a questão pede para encontrarmos a reta tangente, ou seja, a reta que encosta em um único ponto da função no gráfico:
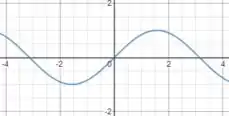
, no caso da letra a) esse ponto é . O valor da função nossa função nesse ponto é:
Passo 2
Agora que já sabemos os valores de x e y no gráfico, devemos encontrar a inclinação dessa reta. Para isso calculamos o valor da derivada nesse mesmo ponto:
No ponto
Passo 3
Já temos tudo para escrever a equação da reta que passa no ponto (0,0) da nossa função seno, a equação da reta tem a forma:
)
Onde T é o valor da inclinação da reta que calculamos antes, que no caso do item a) é 1, e e são as coordenadas do ponto que encontramos onde passa a reta, nossa equação então fica:
)
E isso é:
E a reta no gráfico ficará assim:
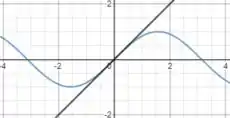
Passo 4
Para as letras b) e c) repetimos o mesmo processo, a letra b) o valor da função em que é
E a inclinação, calculada pela derivada da função:
Tendo o valor da inclinação e do ponto já podemos escrever a equação da reta:
Passo 5
E por fim, na letra c), com a função fica:
E a inclinação, será:
E a equação da reta tangente ao ponto será: