Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.3 - Ex. 7

Use o método das cascas cilíndricas para achar o volume gerado pela rotação ao redor do eixo y da região limitada pelas curvas dadas. Esboce a região e a casca típica.

y = 4 x - 2 2 , y = x 2 - 4 x + 7

Passo 1

Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.

Aqui temos uma situação onde dada uma região, se rotaciona essa região em torno de um eixo e consequentemente obtemos um sólido.

Se girarmos a região R , que será mostrada no próximo passo, em torno do eixo ( y ) , obtemos um sólido ( S ) cujo volume pode ser calculado usando o método das cascas cilíndricas. Abaixo, mostramos uma casca cilíndrica típica para ( S ) .

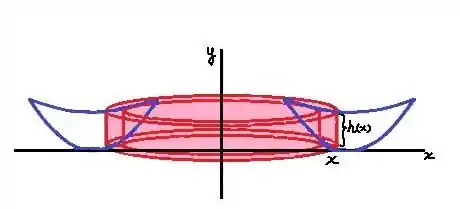
Passo 2

Inicialmente, vamos encontrar as interseções:

y = 4 x - 2 2   y = x 2 - 4 x + 7

Logo,

y = 4 x 2 - 16 x + 16 y = x 2 - 4 x + 7

Igualando, temos:

4 x 2 - 16 x + 16 = x 2 - 4 x + 7

Assim,

x 2 - 4 x + 3 = 0

Então temos o seguinte:

x = 1 ou x = 3

Então vamos aplicar o método das cascas entre os ponto 1 e 3 . Esboçando o gráfico, temos:

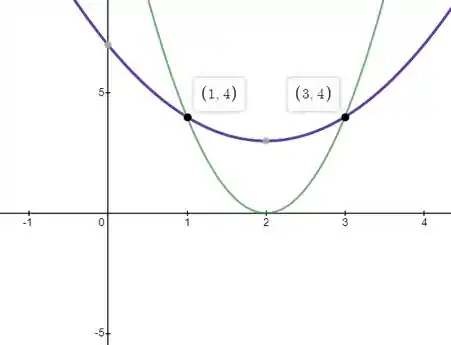
Passo 3

Então o volume ficará o seguinte:

V = ∫ 1 3 2 π x f x d x - ∫ 1 3 2 π x g x d x

Como a função de cima é f x = x 2 - 4 x + 7 e a de baixo é g x = 4 x 2 - 16 x + 16 , temos:

V = ∫ 1 3 2 π x x 2 - 4 x + 7 d x - ∫ 1 3 2 π x 4 x 2 - 16 x + 16 d x

logo,

V = ∫ 1 3 2 π x x 2 - 4 x + 7 - 2 π x 4 x 2 - 16 x + 16 d x  

Fazendo a distributiva e simplificando:

V = - 6 π ∫ 1 3 x 3 - 4 x 2 + 3 x d x

Não esquece: ∫ x n d x   = x n + 1 n + 1 + c   quando   n   ≠ - 1

Passo 4

Integrando, temos o seguinte:

V = - 6 π x 4 4 - 4 x 3 3 + 3 x 2 2 1 3

Aplicando entre esses pontos:

V = - 6 π 3 4 4 - 4 ⋅ 3 3 3 + 3 ⋅ 3 2 2 - 1 4 4 - 4 ⋅ 1 3 3 + 3 ⋅ 1 2 2

Agora é só fazer as contas e correr pro abraço!

V = 16 π

Resposta

V = 16 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja g x =tan 2 ⁡ x x 1 0 , x ≤ π 4 Mostre que x g x = ( tan ⁡ x ) 2; 0 ≤ x ≤ π 4 Determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo y na figura a seguir:
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir: y = x ; y = 2 x ; y = 2
Seja f x =sin ⁡ x x 1 0 , x ≤ π Mostre que x f x = sin ⁡ x0x ≤ π Determine o volume do sólido obtido com a rotação da região sombreada em torno do eixo y na figura a seguir:
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir: x =y; x = - y ; y = 2
Use o método da casca para determinar o volume dos sólidos obtidos com a rotação, em torno do eixo x, das regiões limitadas pelas curvas e retas a seguir: x =2 y - y 2 ; x = 0