Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.9 - Ex. 38
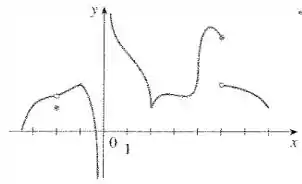
37. O gráfico de 𝑔 é dado.
(a) Em quais números g é descontínua? Por quê?
Em quais números não é diferenciável? Por quê?
Passo 1
Você lembra quais são os casos em que a derivada não existe?
Só olhando no gráfico!!!
Não se desespere, falarei no próximo passo e deixarei o passo para verificarmos onde não é diferenciável.
Caso, a tangente seja vertical ou a gente tenha um bico ou uma descontinuidade naquele ponto, então a função não será diferenciável.
E como verificamos se a função é descontínua?
E temos essa condição também.
No gráfico o que tem que acontecer é:
O limite á esquerda é igual ao da direita que é igual ao valor numérico da função naquele ponto, se a função não respeitar uma dessas condições ela não será contínua.
Passo 2
Lembrando que se uma função não for diferenciável em um ponto, então ela não é contínua.
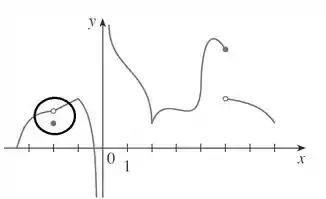
O ponto, que contém o círculo não é contínua pois o limite não é igual ao valor numérico da função, O valor numérico está um pouco para baixo.
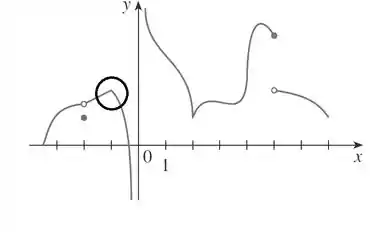
Nesse ponto , a função não é diferenciável, por possuir um “bico” e também não é contínua portanto.
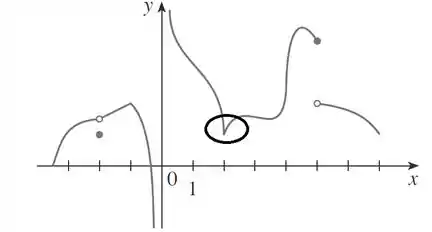
A função possui um “bico” na abscissa , logo a função não é diferenciável e nem contínua nesse ponto.
Passo 3
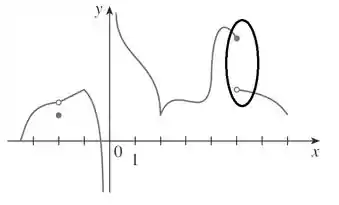
A função não é contínua nesse ponto de abscissa, , pois os limites laterais são diferentes.
Agora para finalizar, falarei de três pontos, em que não conseguiremos afirmar com certeza qual a sua abscissa, porém você pode ter pensando neles
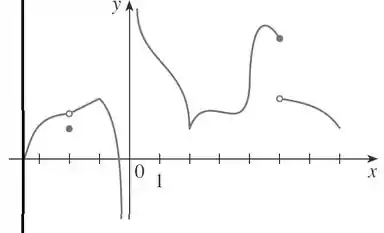
Esse ponto de abscissa de aproximadamente não é diferenciável por conter uma tangente vertical, e por não ser diferenciável, também não é contínua!!
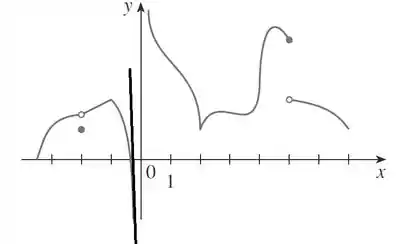
Esse ponto de aproximadamente tem tangente vertical o que torna a função nesse ponto não diferenciável e não continua!
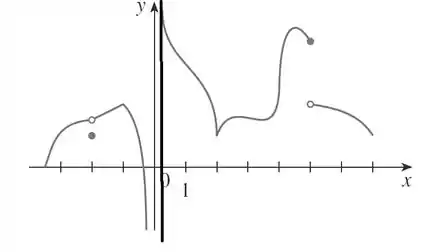
Esse ponto de aproximadamente tem tangente vertical o que torna a função nesse ponto não diferenciável e não continua!
E função não está definida para a origem, logo não é contínua.
Resposta
- ; ; ; ; ; ;
- ; ; ; ;