Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.10 - Ex. 38

Sabe-se que um lado de um triângulo retângulo mede 20 cm de comprimento e o ângulo oposto foi medido como 30°, com um erro possível de ± 1 ° .

(a) Use diferenciais para estimar o erro no cálculo da hipotenusa.

(b) Qual é o erro percentual?

Passo 1

Falaeee, belezinha? Então... a questão quer que a gente calcule o seguinte erro da hipotenusa h :

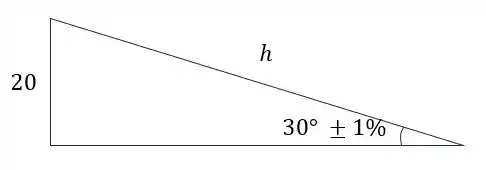
Para isso, devemos utilizar a trigonometria junto com o cálculo diferencial para podermos calcular esse erro.

E aí? Bora lá aplicar? 😉

Passo 2

Item a:

Primeiramente devemos relacionar as variáveis dadas. Temos um ângulo θ , o cateto oposto a ele com 20 cm de comprimento, e a hipotenusa h . Logo, a relação é:

sen ⁡ θ = 20 h

h = 20 sen ⁡ θ

Agora, vamos obter a relação diferencial derivando h em função de θ .

d h = - 20 cos ⁡ θ sen 2 ⁡ θ d θ

Logo, quando o ângulo têm a variação de d θ = 1 ° = π 180 , temos então:

d h = - 20 cos ⁡ 30 ° sen 2 ⁡ 30 ° π 180

d h = - 2 π 3 9 ≈ 1,209199576

Portanto, o erro no cálculo da hipotenusa é de 1,21   c m .

Passo 3

Item b:

O erro percentual E p e r é dado por:

E p e r = Δ h h × 100 % ≈ d h h × 100 %

E p e r = - 20 cos ⁡ θ sen 2 ⁡ θ d θ × 100 % 20 sen ⁡ θ

E p e r = - cos ⁡ θ sen ⁡ θ d θ = - ctg ⁡ θ   d θ

E p e r = - ctg ⁡ ( 30 ° ) π 180 × 100 % = 3,02299894 %

Portando o erro percentual é de aproximadamente 3,023 % .

Resposta

(a) O erro no cálculo da hipotenusa é de 1,21   c m .

(b) O erro percentual é de aproximadamente 3,023 % .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Compare Δ y e d y para os valores dados de x e d x = Δ x . Então esboce um diagrama como o da figura 6, mostrando o segmento de reta com comprimentos d x , d x e Δ y . y = 6 - x 2 ,x = - 2 ,d x = 0,4
Compare Δ y e d y para os valores dados de x e d x = Δ x . Então esboce um diagrama como o da figura 6, mostrando o segmento de reta com comprimentos d x , d x e Δ y . y = x 2 ,x = 1 ,d x = 0,5
Compare Δ y e d y para os valores dados de x e d x = Δ x . Então esboce um diagrama como o da figura 6, mostrando o segmento de reta com comprimentos d x , d x e Δ y . y = 16 x ,x = 4 ,d x = - 1
Use o método de Newton para aproximar a raiz indicada da equação com precisão de seis casas decimais.A raiz positiva de 2 cos ⁡ x = x 4
Use o método de Newton para encontrar todas as soluções da equação corrija até seis casas decimais. 20 . ln ⁡ x = 1 x - 3