Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 3.11 - Ex. 30

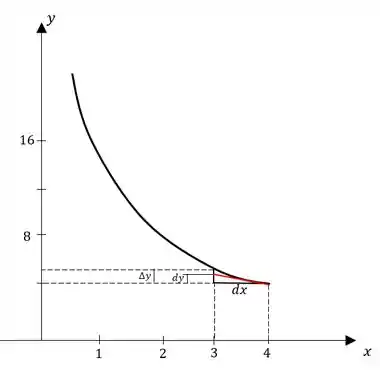
Compare Δ y e d y para os valores dados de x e d x = Δ x . Então esboce um diagrama como o da figura 6, mostrando o segmento de reta com comprimentos d x , d x e Δ y .

y = 16 x ,           x = 4 ,   d x = - 1

Passo 1

A Figura 6 mostra a comparação entre a diferencial d y e a variação verdadeira da função, Δ y , quando acrescentamos um valor d x em x . Vamos fazer o mesmo. Encontramos o diferencial d y de uma função y ( x ) derivando-a e multiplicando pelo diferencial d x :

d y = y ' x   d x

Já a variação verdadeira Δ y é feita simplesmente diminuindo y ( x + Δ x ) de y ( x ) :

Δ y = y x + Δ x - y ( x )

Passo 2

Primeiro vamos calcular o diferencial. Derivando y em relação a x , temos:

y = 16 x

⇒ d y d x = - 16 x 2

Nosso diferencial é então:

d y = - 16 x 2 d x

Então, para x = 4 e d x = - 1 , o diferencial é:

d y = - 16 4 2 - 1 = 1

Passo 3

Agora vamos calcular Δ y . A diferença é entre os pontos x = 4 e x + Δ x = 3 :

Δ y = y 3 - y 4 = 16 3 - 16 4

= 16 4 12 - 3 12 = 16 12 = 4 3 = 1,333 …

⇒ Δ y ≈ 1,33

Podemos ver que os valores de d y e y são bem diferentes, então a aproximação de Δ y por d y não foi boa para esse valor de x e esse valor muito grande de d x .

Passo 4

Então vamos representar d y e Δ y num gráfico. Fazemos o gráfico de y = 16 x e representamos o ponto ( 4 ,   4 ) . Representamos também o ponto - 3 ,     4 / 3 , marcando Δ x = d x e Δ y . Através da reta tangente, achamos d y .

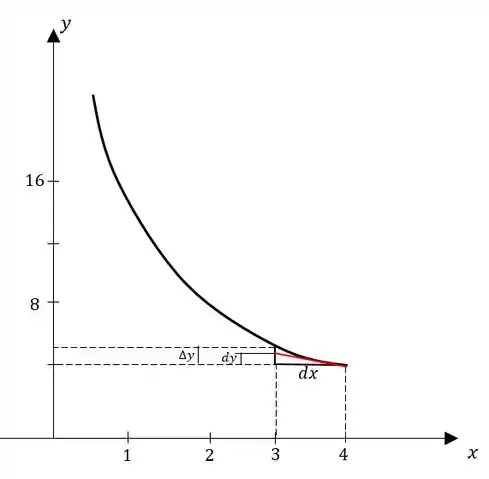
Resposta

d y = 1

Δ y = 4 3 ≈ 1,33

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a diferencial da função.a ) y = t g sqrt(t) b ) y = (1 - v^2)/(1 + v^2)
Encontre a diferencial d y e (b) avalie d y para os valores dados de x e d x . y = 3 + x 2 ,x = 1 ,d x = - 0,1
Use o método de Newton para encontrar todas as raízes da equação corretas até a sexta casa decimal. cos ⁡ x = x
Use o método de Newton para encontrar todas as raízes da equação corretas até a oitava casa decimal. Comece fazendo um gráfico para encontrar a primeira aproximação inicial. e - x 2 = x 2 - x
Use o método de Newton para encontrar todas as raízes da equação corretas até a sexta casa decimal. tg ⁡ x = 1 - x 2