Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.3 - Ex. 47
45-54. Usando a regra de L’Hôspital (Seção 3.6), podemos conferir que:
Nestes exercícios:
a) Use esses limites, se necessário, para obter limites de quando e .
b) Esboce o gráfico de e identifique todos os extremos relativos, os pontos de inflexão e as assíntotas (conforme o caso). Confira seu trabalho com um recurso gráfico.
47.
Passo 1
a) Então galera, temos que a função que nos foi dada é a seguinte:
Se calcularmos os limites de quando e , teremos:
Show! Primeira parte finalizada!
Passo 2
b) Caso não se lembre, para identificarmos os pontos de extremos relativos de uma função devemos fazer uma análise dos pontos críticos da mesma, isto é, analisar os pontos em que ou os pontos em que não existe! Ademais, para identificarmos os pontos de inflexão devemos fazer a mesma análise dos extremos, mas agora para , ok? Vamo que vamo!
Derivando a nossa função, teremos:
Aqui vale ressaltar que utilizamos a regra do quociente para a derivação, ok? Igualando nossa derivada a zero, teremos:
Como não pode ser zero, a única forma disso resultar em zero é se:
Se temos:
E se temos:
Então esses são os nossos possíveis pontos de extremos, galera!
Passo 3
Os pontos de inflexão de uma função são os pontos no qual a função muda de concavidade, ou seja, sai de e vira e vice-versa! Derivando a nossa derivada, teremos:
Simplificando:
Como não pode ser zero, a única forma disso resultar em zero é se:
Utilizando Bhaskara, temos que:
Então esses são os nossos pontos de inflexão, galera!
Passo 4
Substituindo os valores de que encontramos na nossa função, teremos:
Show! Encontramos todos os dados solicitados pelo enunciado, pessoal! Por fim, se plotarmos o gráfico da função, teremos:
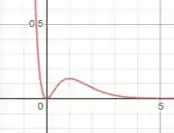
E está aí nossa resolução! 😉
Resposta
a)
b) Pontos de extremos relativos: ;
Pontos de inflexão: ;
Gráfico:
