Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 4.3 - Ex. 37

  1. Encontre os intervalos em que a função é crescente ou decrescente.
  2. Encontre os valores máximo e mínimo locais.
  3. Encontre os intervalos de concavidade e pontos de inflexão.
  4. Use as informações de a)-c) para esboçar o gráfico.

Verifique seu trabalho com uma ferramenta gráfica, se você tiver uma.

h x = x + 1 5 - 5 x - 2

Passo 1

Vamos resolver por ordem dos itens, beleza?

No item a) precisamos achar onde h cresce ou decresce, mas pra isso precisamos da derivada e dos pontos críticos, então vamos encontra-los.

Derivando h , usando a regra da subtração, temos que

h ' x = 5 x + 1 4 - 5

Precisamos achar nossos candidatos a máximo e mínimo, ou seja, pontos críticos.

h ' x = 0

Ou seja,

5 x + 1 4 - 5 = 0

Precisamos que

x + 1 4 = 1

Extraindo a raiz quadrada,

x + 1 2 = 1  

Extraindo a raiz, mais uma vez, temos que

x + 1 = 1   ou   x + 1 = - 1  

O que significa que

x = 0   ou x = - 2  

Então x = 0   e x = - 2   são candidatos a pontos críticos.

Passo 2

Agora, precisamos analisar as proximidades desse ponto para usar o teste da primeira e obter os máximos e mínimos (ou não hahah)

Temos que

  1. h ' x > 0   se   x ∈ - ∞ ,   - 2  
  2. h ' x > 0   se x ∈ 0 , ∞
  3. h ' x < 0   se x ∈ - 2 , 0

(você pode verificar isso pegando números no intervalo que te dei e aplicando na derivada).

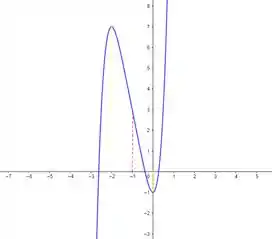
Pelo teste da primeira derivada, h é crescente em - ∞ ,   - 2   e 0 , ∞ e decrescente em 0 ,   - 2   .

Passo 3

Respondendo o item b)...

Vamos usar o item anterior, olha só!

h ( - 2 ) é um máximo local, pois h   sai de crescente para decrescente. E, h 0 =   - 1 é um mínimo local, pois h sai de decrescente para crescente.

Passo 4

Precisamos saber da concavidade da função, beleza? Então vamos calcular a segunda derivada.

Usando a regra da subtração, temos que

h " ( x )   = 20 ( x + 1 ) 3  

Achando o candidato a ponto de inflexão

h ' ' = 0

Ou seja,

  20 ( x + 1 ) 3 = 0

Extraindo a raiz cúbica e isolando x  

x =   - 1  

Temos que esse é nosso candidato a ponto critico

Passo 5

Agora temos que analisar o que acontece nas proximidades do ponto que encontramos no passo anterior, para verificar se ele é mesmo um ponto de inflexão. Vamos lá!

Temos que:

  1. h ' ' x > 0   se   x ∈ - 1 ,   ∞
  2. h ' ' x < 0   se x ∈ - ∞ , - - 1

Pelo teste da segunda derivada, temos um ponto de inflexão em - 1 ,   f - 1 .    

Passo 6

Agora, temos que esboçar o gráfico.

Partiu!

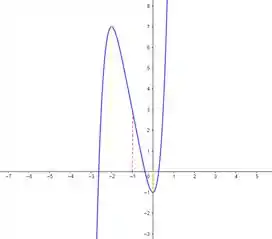
Resposta

Temos que h é crescente em - ∞ ,   - 2   e 0 , ∞ e decrescente em - ∞ ,   - 2   .   h ( - 2 ) é um máximo local. E, h 0 =   - 1 é um mínimo local. Temos um ponto de inflexão em - 1 ,   f - 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Faça o gráfico da curva y = t g - 1 1 x
Faça o gráfico da curva y = ln ⁡ s e n ( x )
Faça o gráfico da curva y = x 3 - x
Faça o gráfico da curva y = x 2 - x + 1 x
Faça o gráfico da função y = x 2 3 + x - 1 2 3 . Em seguida, use a primeira derivada da função para explicar o que você está vendo.