Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.Revisão - Ex. 93
93. Ache área da região no primeiro quadrante limitada pelo eixo y e pelas curvas
Passo 1
Nesse caso sabemos que a área da região requerida será dada pela integral definida da função que está por cima menos a função que está por baixo.
Os limites de integração de x pode ser obtido , um fazendo a intersecção das curvas dadas e o outro utilizando a informação do próprio enunciado quando ele fala que a região é limitada pelo eixo y, ou seja, pela reta x = 0.
Para determinar qual função está por cima e qual está por baixo poderíamos fazer um esboço da região num programa de computador na internet ou mediante a um conhecimento prévio dos gráficos de funções trigonométricas.
Passo 2
O esboço de uma parte região em questão pode ser obtida por meio do programa GeoGebra Online e é o seguinte:
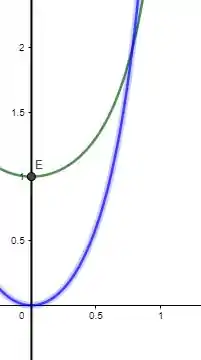
Passo 3
Fazendo a intersecção das duas curvas dada para obter os limites de integração de x temos:
Sendo assim os limites de integração da região em questão é de x = 0 até x = .
Passo 4
Logo, área requerida pelo enunciado pode ser calculada da seguinte forma :