Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 7.1 - Ex. 22
- Achar a inversa b)esboçar o gráfico da função e sua inversa.
22.
Passo 1
Primeiramente precisamos saber que uma função só possue inversa se for biunívoca, ou seja, para cada elemento da imagem existe apenas um elemento do domínio. Caso uma imagem tenha duas imagens do domínio diferentes no intervalo, então ela não é biunívoca, portanto não possui inversa.
Passo 2
Para achar a inversa dessa função precisamos deixar a função tendo como variável o . Desse modo fazemos as seguintes analises.
Podemos chamar agora de função de .
Podemos fazer a seguinte igualdade: . Onde se le a inversa de uma função.
Portanto,
Passo 3
O gráfico dessa função pode ser obtido colocando pontos tanto na inversa quanto na função original:
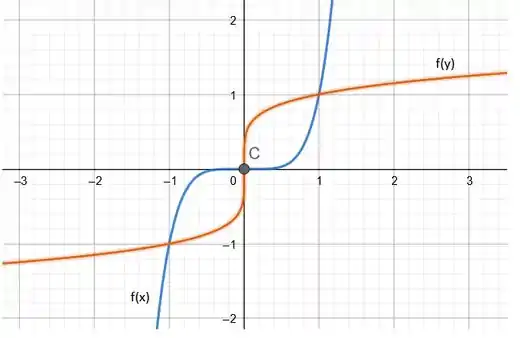
O gráfico em azul representa a função original e a em laranja represente sua inversa.
Resposta
Essa função possui inversa:
Exercícios de Livros Relacionados
Nos Exercícios de 1 a 18, determine se a função é biunívoca. Faça um esboço do gráfico da função. 18 .f x = 1 2 x - 4
Nos Exercícios de 1 a 18, determine se a função é biunívoca. Faça um esboço do gráfico da função.13. G x = sec x , x ∈ 0 , π 2 ∪ π , 3 2 π
Determine se a função dada é biunívoca. Faça um esboço do gráfico da função. f x = 3 - x 2
Determine se a função dada é biunívoca. Faça um esboço do gráfico da função. g x = 1 - x 2
Determine se a função dada é biunívoca. Faça um esboço do gráfico da função. h x = 2s e nx , - π 2 ≤ x ≤ π 2