Ache, com a aproximação de 1 grau, as medidas dos quatro ângulos internos do quadrilátero com vértices em (5,6), (-2,4), (-2,1) e (3,1) e verifique que a soma deles é 360°.
Passo 1
Queremos obter os quatro ângulos do quadrilátero cujos vértices são (5,6), (-2,4), (-2,1) e (3,1).
Para começar, vamos desenhar a situação descrita pelo problema.
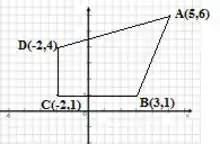
Para achar os ângulos do quadrilátero vamos considerar três partes neste desenho:
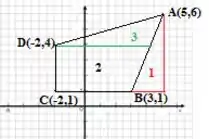
Agora vamos calcular os ângulos para cada parte separadamente.
Passo 2
Parte 1: Para obter os catetos do triângulo retângulo obtido basta calcularmos ∆y e ∆x. O cateto oposto ao ângulo σ é dado por ∆y:
O cateto adjacente ao ângulo σ é dado por ∆x:
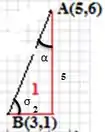
Agora precisamos obter os ângulos α e σ que nos ajudarão a descobrir os ângulos na parte interna do quadrilátero.
Para isso vamos utilizar a tangente, que é dada por:
Para o ângulo σ:
O ângulo é obtido com auxílio de uma calculadora científica, calculando o arco tangente de :
No cálculo de α basta lembrarmos que a soma dos ângulos de um triângulo é 180°. Então:
Parte 2: Nesta parte temos dois ângulos retos e precisamos obter o ângulo a que faz parte do nosso quadrilátero original.
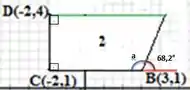
Sabemos que:
Parte 3: Aqui temos outro triângulo retângulo. E precisamos agora obter β e c.
Primeiro, calculamos os catetos do triângulo obtendo ∆y e ∆x. O cateto oposto ao ângulo c é dado por ∆y:
O cateto adjacente ao ângulo c é dado por ∆x:
![]()
Da mesma forma que na parte 1 podemos utilizar a tangente:
O ângulo é obtido com auxílio de uma calculadora científica, calculando o arco tangente de :
No cálculo de β basta lembrarmos que a soma dos ângulos de um triângulo é 180°. Então:
Passo 3
Calculado os ângulos de cada uma das partes e observando a figura somos capazes de obter os ângulos internos do quadrilátero.
Para o vértice A:
Para o vértice B:
Para o vértice C:
Para o vértice D:
Somando os ângulos:
Verificando que a soma dos ângulos internos de um quadrilátero é igual a 360°.