Ache a área da região interior ao gráfico da lemniscata e exterior ao gráfico de .
Passo 1
Para entender melhor a questão é bom ter uma ideia de como é o gráfico.
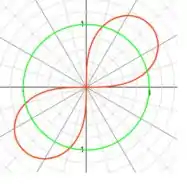
A região referente a área que a questão pede é a que está dentro da lemniscata, vermelho, e fora do círculo, verde.
Passo 2
Note que, como o raio da circunferência é 1 a manipulação matemática para achar os ângulos de intersecção torna-se mais simples. Ou seja, pode igualar direto as duas equações, para obter os ângulos.
Observe que, há dois ângulos no círculo trigonométrico na qual o seno é um meio.
Logo, os ângulos são e .
Esta manipulação só foi possível pois a figura é simétrica, com isso, a área da parte de cima é igual a de baixo, desse modo os outros dois ângulos não precisam ser utilizados no cálculo.
Passo 3
Portanto, e sabendo que a área da região é dada por:
Lembre-se que a primeira equação já está ao quadrado.
Resposta
0.68