Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 8.3 - Ex. 35
Ache a área da região limitada pela curva pelo eixo pelo eixo e pela reta
Passo 1
Desenhando a situação descrita pelo problema:
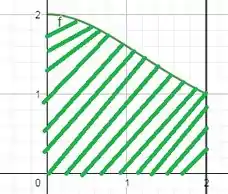
Para calcular a área delimitada pela curva de x indo de 0 até 2 nós precisamos achar a integral desta função:
Segundo o Teorema 8.3.2 as integrais das funções trigonométricas são dadas em função de Sendo assim,
Derivando u:
Substituindo:
Pelo mesmo Teorema:
Passo 2
Usando a calculadora:
Resposta
Exercícios de Livros Relacionados
Nos exercícios de 1 a 30, calcule a integral indefinida.13. ∫ e x t g 4 e x d x
Nos exercícios de 1 a 30, calcule a integral indefinida.12. ∫ sec 5 x d x
Nos exercícios de 15 a 36, calcule a integral indefinida. (25) ∫ 2 - 3 s e n 2 x c o s ( 2 x ) d x
Nos exercícios de 15 a 36, calcule a integral indefinida. (23) ∫ c o t g 5 x + csc 5 x d x
Nos exercícios de 15 a 36, calcule a integral indefinida. (24) ∫ t g 2 x - s e c ( 2 x ) d x