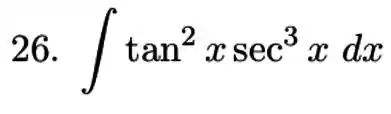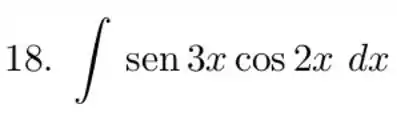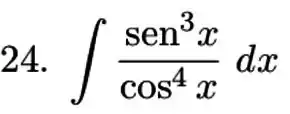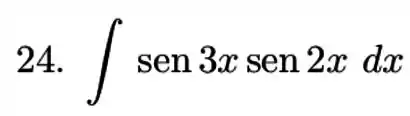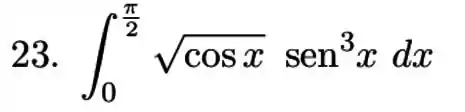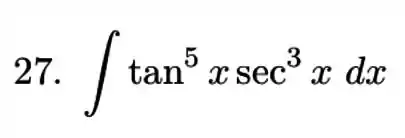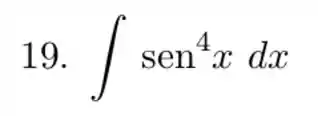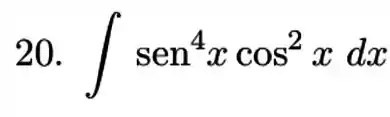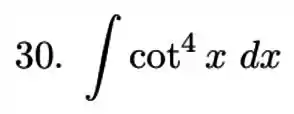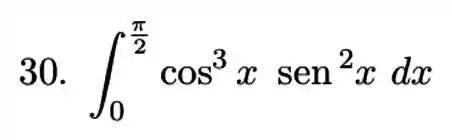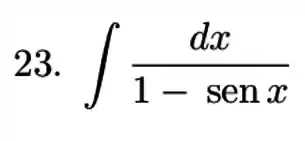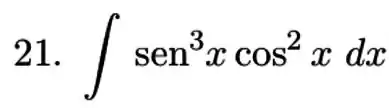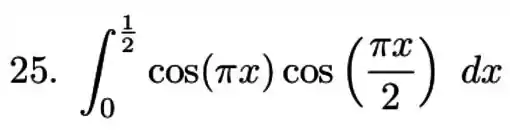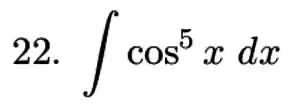Exercícios de Integrais Trigonométricas - Lista de Exercícios Resolvida
Questão 2
Calcule a integral do produto ou quociente de potenciais de funções trigonométricas.
Ver solução completaQuestão 7
Calcule a integral do produto ou quociente de potenciais de funções trigonométricas.
Ver solução completaQuestão 8
(c.1) Mostre que .
(c.2) Utilizando o item (c.1) calcule
(d.1) Mostre que .
(d.2) Utilizando o item (d.1), calcule
Ver solução completaQuestão 9
Calcule as integrais indefinidas das seguintes funções abaixo. Lembrando que as letras A, B C e D, quando presentes representam números da sua matricula conforme instruções descritas no início da prova.
Questão 10
Encontre uma primitiva F, da função abaixo, que satisfaça . Lembrem de achar o valor da constante
Lembrando que as letras A, B, C e D quando presentes representam números da sua matrícula
conforme instruções descritas no início da prova.
Ver solução completaQuestão 11
Calcule as integrais indefinidas das seguintes funções abaixo. Lembrando que as letras A, B C e D, quando presentes representam números da sua matricula conforme instruções descritas no início da prova.
Questão 28
Encontre o comprimento do arco do gráfico da equação dada entre os pontos P e Q ou no intervalo especificado.
c)
Ver solução completaQuestão 36
Calcule a integral do produto ou quociente de potenciais de funções trigonométricas.
Ver solução completaQuestão 37
Calcule a integral indicada, utilizando a técnica de integração por partes
Ver solução completaQuestão 49
Nos exercícios de a , resolva a integral indicada. Em alguns casos será preciso aplicar mais de uma técnica de integração.
4)
Ver solução completaQuestão 72
Calcule a integral do produto ou quociente de potenciais de funções trigonométricas.
Ver solução completaQuestão 78
Um objeto se move ao longo de um trajeto retilíneo. Sua posição, medida em metros , no instante , medido em segundos é dada pela função . Quando , a posição é definida por:
Determine a posição do objeto para e a velocidade do objeto para .
Ver solução completaQuestão 80
Encontre o comprimento do arco do gráfico da equação dada entre os pontos P e Q ou no intervalo especificado.
d)
Ver solução completaQuestão 82
Resolva, desenvolvendo detalhadamente, as integrais abaixo. (Obs.: Não é permitido propor primitivas e derivá-las. As integrais devem ser resolvidas!)
Questão 107
6) Após identificar a técnica apropriada, determine o valor das integrais abaixo.
h)
Ver solução completaQuestão 110
- Determine o valor de real que satisfaz a equação abaixo:
- Utilize o resultado acima e determine o valor da integral abaixo:
Ver solução completaQuestão 121
Lembrando que duas funções que possuem a mesma derivada em um intervalo diferem por uma constante, determine a função que satisfaz as condições abaixo.
Ver solução completaQuestão 122
6) Após identificar a técnica apropriada, determine o valor das integrais abaixo.
f)
Ver solução completaQuestão 123
6) Após identificar a técnica apropriada, determine o valor das integrais abaixo.
e)
Ver solução completaQuestão 124
Após identificar a técnica apropriada, determine o valor das integrais abaixo
Ver solução completaQuestão 129
Ivan, Luciane, Maria Inez, Mykola e Sonia foram encarregados de resolver a integral . A resolução e a resposta de cada estão abaixo.
Ivan.
Luciane.
Maria Inez.
Mykola. Primeiro observemos que . Usando os dois primeiros passos do desenvolvimento da Maria Inez,
Sonia. Além da expressão apontada pelo Mykola para , usaremos também que . Assim,
Quem está certo? Todos obtiveram a mesma resposta?
Ver solução completaQuestão 133
Considere a função
- Determine e (a primeira e segunda derivada de )
- Determine o polimônio de grau 2 que melhor aproxima em torno de .
Questão 137
Calcule as integrais usando substituição trigonométrica. Esboce o triângulo retângulo associado.
Ver solução completaQuestão 139
Calcule cada uma das seguintes integrais e determine se for convergente ou não conforme corresponda:
a)
Ver solução completaQuestão 146
A fórmula de integração por partes normalmente aparece nas tabelas de integrais em uma dessas duas formas:
Vejamos como aplicar a fórmula à integral
- Escolhendo , qual deve ser a escolha para ?
- Para as escolhas do item acima, escreva
- Substitua os valores do item acima na fórmula de integração por partes
- Resolva a integral do enunciado
- Escolhendo , qual deve ser a escolha para ? Calcule e e substitua na fórmula de integração por partes
- A fórmula do item acima não parece ser muito útil. Isso significa que está errada?
Questão 148
Resolva a integral multiplicando e dividindo o integrando pelo conjugado.
Ver solução completaQuestão 162
Verifique as igualdades
; (1)
; (2)
; (3)
e
; (4)
. (5)
utilizando as identidades trigonométricas a seguir
(6)
(7)
; (8)
; (9)
. (10)
Ver solução completa