Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 50
Ache a área da região limitada por um laço da curva , onde n é um número inteiro positivo.
Passo 1
Para entender melhor essa questão precisa-se saber como é o gráfico de uma rosácea.
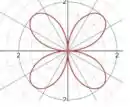
Passo 2
Portanto, para simplificar os cálculos vamos pegar o primeiro laço. Note que, o ponto máximo da primeira folha encontra-se com um ângulo . Desse modo, se sabermos quando vale do inicio até o ponto máximo basta multiplicar por 2 para acharmos a área do laço.
Passo 3
Portanto, e sabendo que a área da região é dada por:
Resposta
Exercícios de Livros Relacionados
Transformar a seguinte equação para coordenadas cartesianas. r = 2 sin θ
Transformar a seguinte equação para coordenadas polares. y + x = 0
Usar r0 e 0 ≤ θ ≤ 2 π Para escrever os pontos P 1 3 , - 1 e P 2 - 2 ,- 2 em coordenadas polares.
Usar r0 e 0 ≤ θ ≤ 2 π Para escrever os pontos P 1 3 , - 1 e P 2 - 2 ,- 2 em coordenadas polares.
Encontrar um par de coordenadas polares do seguinte ponto: 1 , - 1