Enunciado
Álgebra Linear e Geometria Analítica - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.2 - Ex. 10
Ache o comprimento das medianas do triângulo com vértices , e .
Passo 1
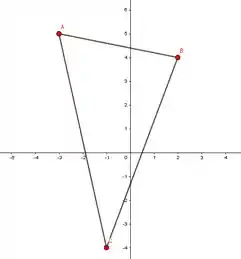
Inicialmente vamos marcar os pontos , e no plano cartesiano e fazer o esboço do triângulo.
Passo 2
Sejam , e o pontos médios dos segmentos , e , respectivamente. Vamos determinar cada um desses pontos. Para o segmento , temos o ponto , e logo:
Show de bola, agora continuamos com essa ideia. Pro ponto como ponto médio de teremos:
E pra fechar, sendo o ponto médio de :
Vamos ter então três medianas, que seriam os segmentos , e
Passo 3
Para sabermos o comprimento das medianas basta encontramos a distância de cada vértice ao ponto médio do respectivo lado oposto.
Seja:
A distância entre e é dada por:
Seja:
A distância entre e é dada por:
Seja:
A distância entre e é dada por:
Resposta
O comprimento da mediana referente ao vértice A é , da mediana referente ao vértice B é e da mediana referente ao vértice C é .