Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 56
Ache a equação polar da cônica que satisfaz as condições dadas e faça um esboço do gráfico. Um foco na origem; um vértice em (6, ); .
Passo 1
E ai, vamos começar a calcular? Errado!!! Muito cuidado, sempre que tivermos qualquer questão de gemotria analítica devemos fazer um esboço de seja o que a questão der e fazer uma análise do nosso desenho. Nesse caso temos o ponto de um dos vértices () e o ponto do foco () lembrando que essas coordenadas estão no sistema de coordenadas polares.
Opa, não vamos deixar de lado a excentricidade que a questão nos deu. Observando que ela é menor do que zero () temos a valiosa informação que estamos falando de uma elipse! Te dando mais uma dica sobre as cônicas, você deve olhar para o foco como se ele estivesse puxando a curva pra ele.
Olhando para aquele nosso esboço percebemos que o foco está abaixo do vértice, logo ele tentará puxar a figura pra baixo, formando um elipse vertical que, se me lembro bem, possui a seguinte fórmula:
Passo 2
Se um dos vértices é o ponto () e sabemos o valor da excentricidade (), então só mandar ver substituindo as variáveis da equação (1):
Passo 3
Agora que conhecemos o valor de e o valor de não ta faltando mais nada pra responder a primeira parte da questão. Pega aquela fórmula (1) e é só substituir os valores que descobrimos nela:
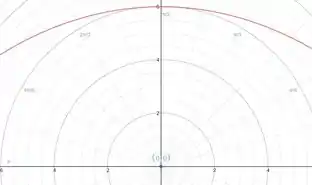
Passo 4
Pra acabar de vez vamos só preparar um eixo de coordenadas polares e substituir alguns valores de na equação da elipse (2) e descobrir o raio correspondente a cada um desses agulos para fazer a marcação. Mas não inventa moda, use os ângulos mais fáceis e que estamos habituados a usar: e seus complementares.