Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 10.Revisão - Ex. 39
Ache todos os pontos de intercecção dos gráficos das duas curvas dadas.
Passo 1
Olhando essas funções, a gente percebe que elas se parecem com algo que a gente já estudou antes, não?
Essa primeira função corresponde a um cardioide com o parâmetro a igual a 2.
Essa segunda função corresponde a uma circuferencia achatada nos polos.
Passo 2
Para acharmos os pontos em comum, precisamos igualar as duas, mas algo engraçado acontece.
A única solução para essa equação é a de que elas são iguais somente em 0. Ou seja, elas só se encontram na origem.
Passo 3
Observe a imagem:
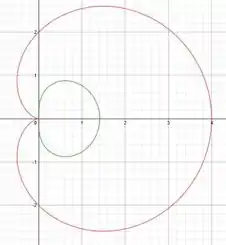
Resposta
Só se tocam na origem.
Exercícios de Livros Relacionados
Plote o ponto cujas coordenadas cilíndricas são dadas. Depois, determine as coordenadas retangulares do ponto. 5 , π 6 , 6
O que são coordenadas cilíndricas? Para que tipo de superfícies elas fornecem uma descrição conveniente?
Converta de coordenadas retangulares para coordenadas cilíndricas 3,3 , - 2
Converta de coordenadas retangulares para coordenadas cilíndricas - 1 , - 3 , 2
Converta de coordenadas retangulares para coordenadas cilíndricas 3,4 , 5