Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.11 - Ex. 17

Nos exercícios 9 a 32, esboçar o gráfico das curvas dadas em coordenadas polares.

17. r = a ± b s e n θ

a = 2 e b = 3 ; a = 3 e b = 2 ; a = b = 2

Passo 1

As coordenadas polares são um sistema bidimensional de coordenadas, alternativo ao sistema cartesiano.

Cada ponto no sistema de coordenadas polares é representado por um raio (uma distância) e um ângulo (em graus ou radianos), em relação a origem – geralmente o ponto (0,0), denominado polo.

Esses pontos vão ser sempre representados na forma ( r , θ ) , em que a distância r pode ou não ser expressa como uma função do ângulo θ .

Passo 2

Com o auxílio do programa Geogebra, digitamos, na função de malha para coordenadas polares, os pontos ( a + b s e n θ ,   θ ) e ( a - b s e n θ ,   θ ) , com a = 2 e b = 3 temos os seguintes gráficos para as respectivas equações polares, na ordem que aparecem:

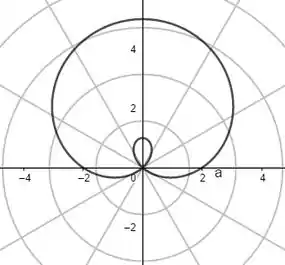
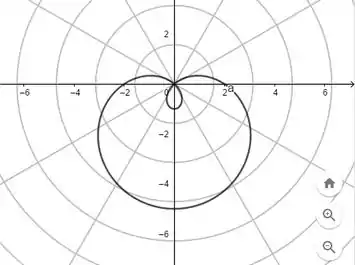
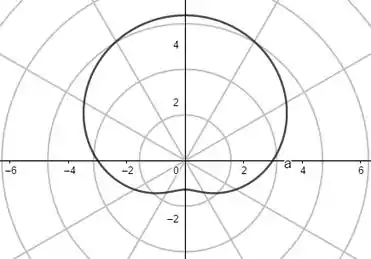
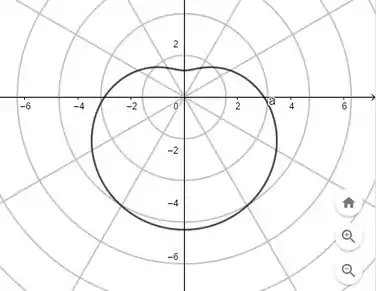
( a + b s e n θ ,   θ ) e ( a - b s e n θ ,   θ ) , com a = 3 e b = 2 , respectivamente, teremos:

Por fim, para ( a + b s e n θ ,   θ ) e ( a - b s e n θ ,   θ ) , com a = b = 2 , respectivamente, teremos:

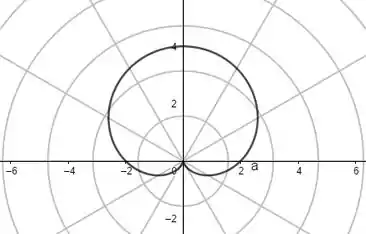
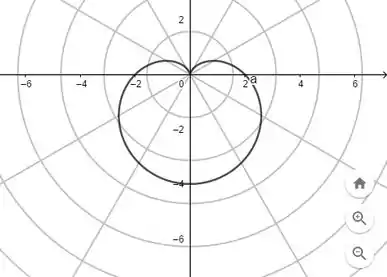
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os planetas se movem ao redor do Sol em órbitas elípticas com o Sol em um dos focos. As posições de um planeta que estão mais próximas ou mais afastadas do Sol são chamadas respectivamente periélio e
a) Encontre a excentricidade, b) identifique a cônica, c) dê uma equação da diretriz e d) esboce a cônica. r = 6 3 + 2s e nθ
12- a) Encontre a excentricidade, b) identifique a cônica, c) dê uma equação da diretriz e d) esboce a cônica. r = 4 2 - 3 cos ⁡ θ
O que são coordenadas esféricas? Para que tipo de superfícies elas fornecem uma descrição conveniente?
Plote o ponto cujas coordenadas cilíndricas são dadas. Depois, determine as coordenadas retangulares do ponto. 5 , π 6 , 6